题目内容
为预防X病毒爆发,某生物技术公司研制出一种X病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
| 分组 |  组 组 | 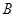 组 组 |  组 组 |
| 疫苗有效 | 673 | 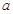 | 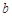 |
| 疫苗无效 | 77 | 90 | 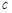 |
已知在全体样本中随机抽取1个,抽到
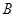 组疫苗有效的概率是0.33.
组疫苗有效的概率是0.33.(1)现用分层抽样的方法在全体样本中抽取360个测试结果,应在
 组抽取样本多少个?
组抽取样本多少个?(2)已知
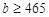 ,
,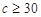 ,求通过测试的概率.
,求通过测试的概率.
(1)90 (2)
解析试题分析:(I)根据分层抽样的定义,按每层中的比例即可计算出 组抽取样本的个数;(II)由(I)
组抽取样本的个数;(II)由(I) ,再结合题设条件
,再结合题设条件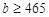 ,
,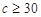 列举出所有可能的
列举出所有可能的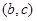 组合的个数及没有通过测试的
组合的个数及没有通过测试的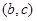 组合的个数,再由概率公式及概率的性质求出通过测试的概率.
组合的个数,再由概率公式及概率的性质求出通过测试的概率.
(I)∵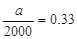 ,∴
,∴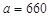 ,
,
∵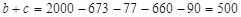 ,
,
∴ 应在 组抽取样个数是
组抽取样个数是 (个).
(个).
(II)∵ ,
,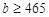 ,
,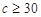 ,
,
∴(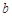 ,
,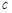 )的可能性是 (465,35),(466,34),(467,33),(468,32),(469,31),(470,30),
)的可能性是 (465,35),(466,34),(467,33),(468,32),(469,31),(470,30),
若测试没有通过,则 ,
,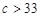 ,
,
(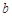 ,
,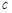 )的可能性是(465,35),(466,34),
)的可能性是(465,35),(466,34),
通过测试的概率是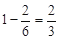 .
.
考点:1、分层抽样;2.、古典概型;3、估测能力.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
某人摆一个摊位卖小商品,一周内出摊天数x与盈利y(百元),之间的一组数据关系见表:
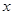 | 2 | 3 | 4 | 5 | 6 |
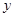 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
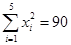 ,
,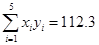 ,
,(1)在下面坐标系中画出散点图;

(2)计算
 ,
,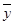 ,并求出线性回归方程;
,并求出线性回归方程;(3)在第(2)问条件下,估计该摊主每周7天要是天天出摊,盈利为多少?
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
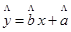
(2)试根据已求出的线性回归方程,预测记忆力为9的同学的判断力.
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于 小于
小于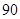 为二等品,小于
为二等品,小于 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利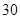 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
| 测试指标 | 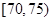 | 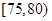 | 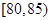 | 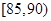 | 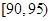 | 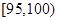 |
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算甲生产一件产品A,给工厂带来盈利不小于30元的概率;
(2)若甲一天能生产20件产品A,乙一天能生产15件产品A,估计甲乙两人一天生产的35件产品A中三等品的件数.
在某种产品表面进行腐蚀性刻线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值,如下表:
| x/s | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 90 | 120 |
| y/μm | 6 | 10 | 10 | 13 | 16 | 17 | 19 | 23 | 25 | 29 | 46 |

 ,
,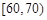 ,
, ,
,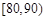 ,
,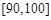 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在

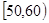 ,2;
,2;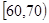 ,7;
,7;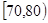 ,10;
,10;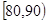 ,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.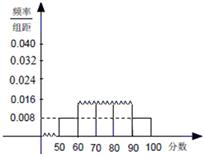
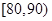 的矩形的高;
的矩形的高;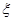 ,求
,求