题目内容
某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，其可见部分如下，据此解答如下问题：
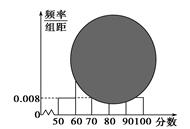
（1）计算频率分布直方图中[80,90)间的矩形的高；
（2）若要从分数在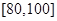
之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份试卷的分数在
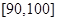之间的概率；
（3）根据频率分布直方图估计这次测试的平均成绩．
（1）0.016;（2）0.6;（3）73.8
解析试题分析：（1）有茎叶图以及频率分布直方图，可知在50-60段的人数和所占的频率，即可求出该班参加数学测试的人数.80-90段的人数有总人数减去其他四段的人数和，计算出频率以及频率除以组距的值，即得到频率直方图的高. 以下是某地搜集到的新房屋的销售价格 某人摆一个摊位卖小商品，一周内出摊天数x与盈利y(百元)，之间的一组数据关系见表： 近年来，我国很多城市都出现了严重的雾霾天气．为了更好地保护环境，2012年国家环保部发布了新修订的《环境空气质量标准》,其中规定:居民区 的PM2.5的年平均浓度不得超过35微克/立方米.某城市环保部门在2014年1月1日到 2014年3月31日这90天对某居民区的PM2. 5平均浓度的监测数据统计如下: 某中学一位高三班主任对本班 某公司生产产品A，产品质量按测试指标分为：指标大于或等于90为一等品，大于或等于
（2）由（1）可得在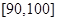的人数总共为6人，从中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份试卷的分数在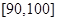之间的概率的计算，可通过计算没有一份在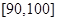内，再用总数1减去即可.
（3）计算出各段的频率，再将各段的中点值乘以本段的频率相加即可.
（1）分数在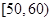
的频率为
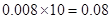，由茎叶图知：分数在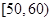之间的频数为
，所以全班人数为
， 2分
∴分数在
之间的人数为
人，则对应的频率为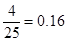
． 3分
所以间的矩形的高为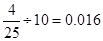
． 4分
（2）将之间的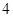
个分数编号为
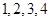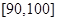， 之间的个分数编号为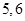
，
在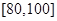之间的试卷中任取两份的基本事件为：
，
，
，
，
， 
，
，
，
，
，
，
，
，
，
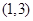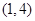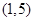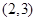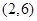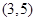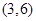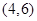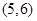共
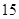个． 6分
其中，至少有一份在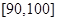之间的基本事件有
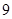个，
故至少有一份分数在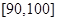之间的概率是
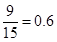． 8分.
（3）全班人数共
人，根据各分数段人数计算得各分数段的频率为：分数段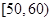 
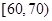
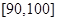
频率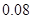 
经纶学典课时作业系列答案
浙江名卷系列答案
励耘活页系列答案
（万元）和房屋的面积
（
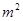）的数据 ，若由资料可知对呈线性相关关系。80 90 100 110 120 y 48 52 63 72 80
试求:（1）线性回归方程；
（2）根据（1）的结果估计当房屋面积为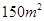
时的销售价格.
参考公式：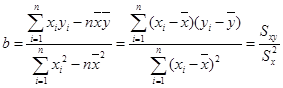
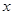
2 3 4 5 6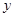 
2.2 3.8 5.5 6.5 7.0
已知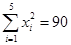
，
，
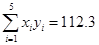(1)在下面坐标系中画出散点图；
(2)计算
，
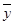，并求出线性回归方程；
(3)在第(2)问条件下，估计该摊主每周7天要是天天出摊，盈利为多少? 组别 PM2.5浓度（微克/立方米） 频数（天） 第一组 （0,35] 24 第二组 (35,75] 48 第三组 (75,115] 12 第四组 >115 6
（1）在这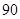
天中抽取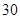
天的数据做进一步分析,每一组应抽取多少天?
（2）在(I)中所抽取的样本PM2. 5的平均浓度超过75(微克/立方米)的若干天中,随 机抽取2天,求至少有一天平均浓度超过115(微克/立方米)的概率. 
名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示: 积极参加班级工作 不太主动参加班级工作 合计 学习积极性高 18 7 25 学习积极性一般 6 19 25 合计 24 26 50
(1)如果随机调查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
(2)学生的积极性与对待班级工作的态度是否有关系?说明理由. 
小于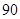
为二等品，小于为三等品，生产一件一等品可盈利50元，生产一件二等品可盈利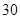
元，生产一件三等品亏损10元．现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测，检测结果统计如下：测试指标
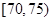
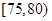
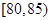
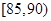
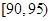
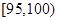
甲
3
7
20
40
20
10
乙
5
15
35
35
7
3
根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率．
（1）计算甲生产一件产品A，给工厂带来盈利不小于30元的概率；
（2）若甲一天能生产20件产品A，乙一天能生产15件产品A，估计甲乙两人一天生产的35件产品A中三等品的件数.
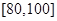之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份的分数在
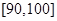之间的概率；
的值；
与
中的学生人数；
的学生中人选2人，求此2人的成绩都在