题目内容
由某种设备的使用年限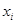 (年)与所支出的维修费
(年)与所支出的维修费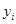 (万元)的数据资料算得如下结果,
(万元)的数据资料算得如下结果,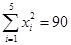 ,
,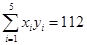 ,
,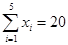 ,
,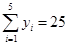 .
.
(1)求所支出的维修费y对使用年限x的线性回归方程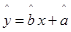 ;
;
(2)①判断变量x与y之间是正相关还是负相关;
②当使用年限为8年时,试估计支出的维修费是多少.
(附:在线性回归方程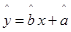 中,)
中,)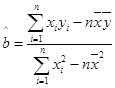 ,
,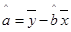 ,其中
,其中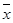 ,
, 为样本平均值.)
为样本平均值.)
(1)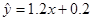 ;(2)变量
;(2)变量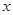 与
与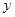 之间是正相关,
之间是正相关,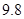 万元.
万元.
解析试题分析:本题主要考查线性回归方程、变量间的正相关和负相关的判断等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,利用已知的数值及公式先计算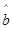 ,再利用
,再利用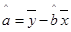 计算
计算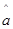 ,从而得到线性回归方程;第二问,①在
,从而得到线性回归方程;第二问,①在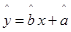 中,当
中,当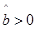 时,变量x与y之间是正相关,当
时,变量x与y之间是正相关,当 时,变量x与y之间是负相关,本题是正相关;②使用年限即x的值,而维修费用是y的值,代入回归方程中求函数值y即可.
时,变量x与y之间是负相关,本题是正相关;②使用年限即x的值,而维修费用是y的值,代入回归方程中求函数值y即可.
(1)∵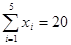 ,
,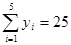 ,∴
,∴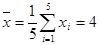 ,
,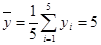
∴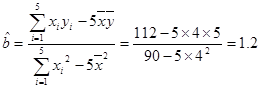 3分
3分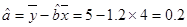 5分
5分
∴线性回归方程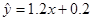 . 6分
. 6分
(2)①由(1)知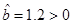 ,∴变量
,∴变量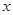 与
与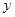 之间是正相关. 9分
之间是正相关. 9分
②由(1)知,当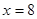 时,
时,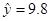 (万元),即使用年限为
(万元),即使用年限为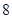 年时,支出的维修费约是
年时,支出的维修费约是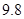 万元.
万元.
12分
考点:线性回归方程、变量间的正相关和负相关的判断.

某班主任对全班50名学生的积极性和对待班级工作的态度进行了调查,
统计数据如下表所示:
| | 积极参加班级工作 | 不太积极参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
试运用独立性检验的思想方法分析:学生的学习积极性与对待班级的态度是否有关系?
|
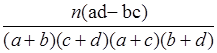
| P(K2≥k0 ) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
近年来,我国很多城市都出现了严重的雾霾天气.为了更好地保护环境,2012年国家环保部发布了新修订的《环境空气质量标准》,其中规定:居民区 的PM2.5的年平均浓度不得超过35微克/立方米.某城市环保部门在2014年1月1日到 2014年3月31日这90天对某居民区的PM2. 5平均浓度的监测数据统计如下:
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) |
| 第一组 | (0,35] | 24 |
| 第二组 | (35,75] | 48 |
| 第三组 | (75,115] | 12 |
| 第四组 | >115 | 6 |
(1)在这
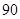 天中抽取
天中抽取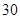 天的数据做进一步分析,每一组应抽取多少天?
天的数据做进一步分析,每一组应抽取多少天?(2)在(I)中所抽取的样本PM2. 5的平均浓度超过75(微克/立方米)的若干天中,随 机抽取2天,求至少有一天平均浓度超过115(微克/立方米)的概率.
某学校高一年学生在某次数学单元测试中,成绩在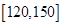 的频数分布表如下:
的频数分布表如下:
| 分数 |  | 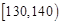 | 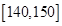 |
| 频数 | 60 | 20 | 20 |
(1)用分层抽样的方法从成绩在
 ,
,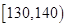 和
和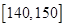 的同学中共抽取
的同学中共抽取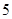 人,其中成绩在
人,其中成绩在 的有几人?
的有几人?(2)从(1)中抽出的
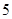 人中,任取
人中,任取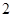 人,求成绩在
人,求成绩在 和
和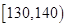 中各有
中各有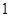 人的概率?
人的概率? 从发生汽车碰撞事故的司机中抽取2 000名司机.根据他们的血液中是否含有酒精以及他们是否对事故负有责任.将数据整理如下:
| | 有责任 | 无责任 | 合计 |
| 有酒精 | 650 | 150 | 800 |
| 无酒精 | 700 | 500 | 1 200 |
| 合计 | 1 350 | 650 | 2 000 |


 ,
,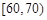 ,
, ,
,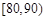 ,
,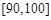 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
