Question

【题目】如图，在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD是边长2的正方形，E，F分别为线段DD1，BD的中点．

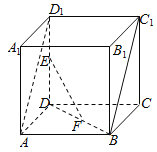
（1）求证：EF∥平面ABC1D1；

（2）AA1=2，求异面直线EF与BC所成的角的大小．

Answer 1

【答案】（1）见解析； （2）.

【解析】

（1）连结BD1，推导出EF∥D1B，由此能证明EF∥平面ABC1D1;（2）由EF∥BD1，知∠D1BC是异面直线EF与BC所成的角（或所成角的补角），由此能求出异面直线EF与BC所成的角的大小.

（1）连结BD1，在△DD1B中，E、F分别是D1D、DB的中点，

∴EF是△DD1B的中位线，∴EF∥D1B，∵D1B平面ABC1D1，EF平面ABC1D1，∴EF∥平面ABC1D1．

（2）∵AA1=2，AB=2，EF∥BD1，∴∠D1BC是异面直线EF与BC所成的角（或所成角的补角），

在直四棱柱ABCD﹣A1B1C1D1中，BC⊥平面CDD1C1，CD1平面CDD1C1，∴BC⊥CD1．

在Rt△D1C1C中，BC=2，CD1=2，D1C⊥BC，∴tan∠D1BC=，∴∠D1BC=60°，

∴异面直线EF与BC所成的角的大小为60°．