题目内容
在 中,已知
中,已知 .
.
(1)求证: ;
;
(2)若 求角A的大小.
求角A的大小.
(1)证明见解析;(2) .
.
解析试题分析:(1)已知的向量的数量积,要证明的是角的关系,故我们首先运用数量积定义把已知转化为三角形的边角关系,由已知可得 ,即
,即 ,考虑到求证式只是角的关系,因此我们再应用正弦定理把式子中边的关系转化为角的关系,即有
,考虑到求证式只是角的关系,因此我们再应用正弦定理把式子中边的关系转化为角的关系,即有 ,而这时两边同除以
,而这时两边同除以 即得待证式(要说明
即得待证式(要说明 均不为零).(2)要求解
均不为零).(2)要求解 的大小,一般是求出这个角的某个三角函数值,本题应该求
的大小,一般是求出这个角的某个三角函数值,本题应该求 ,因为(1)中有
,因为(1)中有 可利用,思路是
可利用,思路是 .
.
试题解析:(1)∵ ,∴
,∴ ,
,
即 . 2分
. 2分
由正弦定理,得 ,∴
,∴ . 4分
. 4分
又∵ ,∴
,∴ .∴
.∴ 即
即 . 6分
. 6分
(2)∵ ,∴
,∴ .∴
.∴ .8分
.8分
∴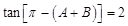 ,即
,即 .∴
.∴ . 10分
. 10分
由 (1) ,得 ,解得
,解得 . 12分
. 12分
∵ ,∴
,∴ .∴
.∴ . 14分
. 14分
考点:(1)向量的数量积的定义与正弦定理;(2)已知三角函数值,求角.

练习册系列答案
相关题目
 .
.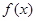 的最小正周期和图像的对称轴方程;
的最小正周期和图像的对称轴方程; 上的值域.
上的值域. ;
; 为第二象限角,化简
为第二象限角,化简 .
. ,
, ,且
,且 。
。 )取最大值时,判断三角形ABC的形状。
)取最大值时,判断三角形ABC的形状。 的最小正周期为
的最小正周期为 .
. 的对称轴方程;
的对称轴方程;  ,求
,求 的值.
的值. (
( )的最小正周期为
)的最小正周期为 .求函数
.求函数 的单调增区间;
的单调增区间; 中,角
中,角 对边分别是
对边分别是 ,且满足
,且满足 .若
.若 ,
, .求角
.求角 的大小和边b的长.
的大小和边b的长. 为钝角的的三角形
为钝角的的三角形 内角
内角 的对边分别为
的对边分别为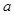 、
、 、
、 ,
, ,且
,且 与
与 垂直.
垂直. 的取值范围
的取值范围 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为
 ,
, ,求
,求 的值.
的值. 中,角
中,角 的对边分别为
的对边分别为 ,
, .
. 的大小;
的大小;
 的值域
的值域