题目内容
在 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为
(Ⅰ)叙述并证明正弦定理;
(Ⅱ)设 ,
, ,求
,求 的值.
的值.
(Ⅰ)证明见解析;(Ⅱ) 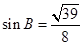 .
.
解析试题分析:(Ⅰ)正弦定理: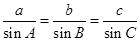 ,利用三角形的外接圆证明正弦定理. 设
,利用三角形的外接圆证明正弦定理. 设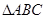 的外接圆的半径为
的外接圆的半径为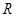 ,连接
,连接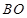 并延长交圆
并延长交圆 于点
于点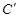 ,则
,则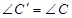 ,直径所对的圆周角
,直径所对的圆周角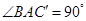 ,在直角三角形
,在直角三角形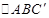 中,
中,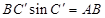 ,从而得到
,从而得到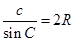 ,同理可证
,同理可证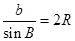 ,
,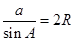 ,则正弦定理得证;(Ⅱ)先由正弦定理将
,则正弦定理得证;(Ⅱ)先由正弦定理将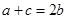 化为
化为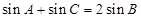 ①,再依据和差化积公式,同角三角函数间的关系,特殊角的三角函数值将①式化简,得到
①,再依据和差化积公式,同角三角函数间的关系,特殊角的三角函数值将①式化简,得到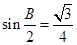 ,则
,则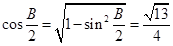 ,再由二倍角公式
,再由二倍角公式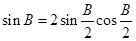 求解.
求解.
试题解析:(Ⅰ) 正弦定理: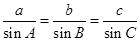 .
.
证明:设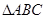 的外接圆的半径为
的外接圆的半径为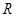 ,连接
,连接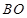 并延长交圆
并延长交圆 于点
于点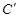 ,如图所示:
,如图所示: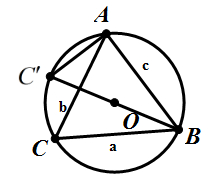
则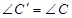 ,
,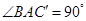 ,在
,在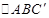 中,
中,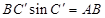 ,即
,即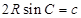 ,则有
,则有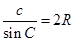 ,同理可得
,同理可得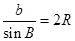 ,
,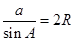 ,所以
,所以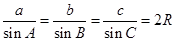 .
.
(Ⅱ)∵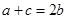 ,由正弦定理得,
,由正弦定理得,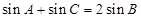 ,
, ,
,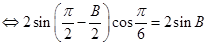 ,
,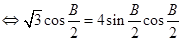 ,
,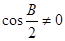 ,
,
解得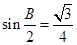 ,
,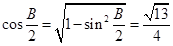 ,
,
∴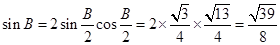 .
.
考点:1.正弦定理;2.解三角形;3.同角三角函数间的关系;4.和差化积公式;5.二倍角公式

练习册系列答案
相关题目
 中,已知
中,已知 .
. ;
;  求角A的大小.
求角A的大小. 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 .
. 的值;
的值; ,
, ,求
,求 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, 的值;
的值; ,
, ,求
,求 的值.
的值. 的顶点在原点,始边与
的顶点在原点,始边与 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点 .
. 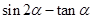 的值;
的值; ,求函数
,求函数 在区间
在区间 上的取值范围.
上的取值范围.  的最大值为
的最大值为 ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为 .
.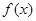 的解析式;
的解析式; ,求
,求 的值.
的值. ,
, .
. 为何值时,
为何值时, 取得最大值,并求出其最大值;
取得最大值,并求出其最大值; ,
, ,求
,求 的值.
的值. 的图象(部分)如图所示.
的图象(部分)如图所示.
 的解析式;
的解析式; ,求函数
,求函数 中,三个内角
中,三个内角 所对的边分别为
所对的边分别为
 已知
已知 ,
, .
.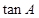 ;
; 求
求 的值.
的值.