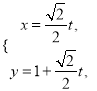Question

【题目】以下四个命题中：
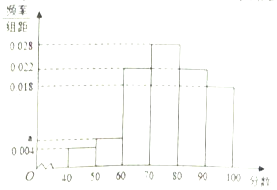
①某地市高三理科学生有15000名，在一次调研测试中，数学成绩 服从正态分布 ，已知 ，若按成绩分层抽样的方式抽取100份试卷进行分析，则应从120分以上（包括120分）的试卷中抽取 份；
②已知命题 ，则 ： ；
③在 上随机取一个数 ，能使函数 在 上有零点的概率为 ；
④设 ，则“ ”是“ ”的充要条件.
其中真命题的序号为.

Answer 1

【答案】②③
【解析】①∵
∴应从120分以上（包括120分）的试卷中抽取100×0.1=10（份），故①为假命题；
②由全称命题的否定是特称命题知， 为 ，故②为真命题；
③若 有零点，则 ，解得m≥2或m≤-2，由几何概率计算公式可得在 上随机去一个数m，能使函数 在R上有零点的概率为 ，故③为真命题；
④ ，所以“ ”是“ >1”的充分不必要条件，故④为假命题.
故填②③.
【考点精析】利用函数的零点与方程根的关系对题目进行判断即可得到答案，需要熟知二次函数的零点：（1）△＞0，方程 有两不等实根，二次函数的图象与 轴有两个交点，二次函数有两个零点;（2）△＝0，方程 有两相等实根（二重根），二次函数的图象与 轴有一个交点，二次函数有一个二重零点或二阶零点;（3）△＜0，方程 无实根，二次函数的图象与 轴无交点，二次函数无零点．