题目内容
【题目】命题![]() 方程
方程![]() 表示双曲线;命题
表示双曲线;命题![]() 不等式
不等式![]() 的解集是
的解集是![]() .
. ![]() 为假,
为假, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】试题分析:由命题![]() 方程
方程![]() 表示双曲线,求出
表示双曲线,求出![]() 的取值范围,由命题
的取值范围,由命题![]() 不等式
不等式![]() 的解集是
的解集是![]() ,求出
,求出![]() 的取值范围,由
的取值范围,由![]() 为假,
为假, ![]() 为真,得出
为真,得出![]() 一真一假,分两种情况即可得出
一真一假,分两种情况即可得出![]() 的取值范围.
的取值范围.
试题解析:
![]() 真
真 ![]()
![]() ,
,
![]() 真
真 ![]() 或
或![]()
![]()
∴![]()
![]() 真
真![]() 假
假 ![]()
![]() 假
假![]() 真
真 ![]()
∴![]() 范围为
范围为![]()
【题型】解答题
【结束】
18
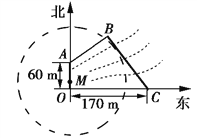
【题目】如图,设![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 是
是![]() 在
在![]() 轴上的投影,
轴上的投影, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.

(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)求过点![]() 且斜率为
且斜率为![]() 的直线被
的直线被![]() 所截线段的长度.
所截线段的长度.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】试题分析:(1)由题意可知:M的坐标为(x,y),P的坐标为(x',y'),则![]() ,得
,得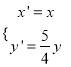 ,代入
,代入![]() ,整理得:
,整理得: ![]() .
.
(2)设直线方程为: ![]() ,代入椭圆方程,由韦达定理可知:x1+x2=3,x1x2=-8,弦长公式:丨AB丨=
,代入椭圆方程,由韦达定理可知:x1+x2=3,x1x2=-8,弦长公式:丨AB丨=![]() 即可求得直线被C所截线段的长度.
即可求得直线被C所截线段的长度.
试题解析:
(1)设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,由已知得
,由已知得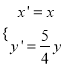 .
.
∵![]() 在圆上,
在圆上, ![]() ,
,
即![]() ,整理得
,整理得![]() ,即
,即![]() 的方程为
的方程为![]() .
.
(2)过点![]() 且斜率为
且斜率为![]() 的直线方程为
的直线方程为![]() ,
,
设直线与![]() 的交点为
的交点为![]() ,
, ![]() ,将直线方程
,将直线方程![]() 代入
代入![]() 的方程,
的方程,
得![]() ,即
,即![]() .
.
∴x1+x2=3,x1x2=-8∴线段![]() 的长度为
的长度为
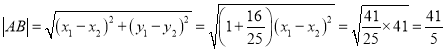 .
.
∴直线被![]() 所截线段的长度为
所截线段的长度为![]() .
.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目