题目内容
16.如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是 线段BE,DC的中点.
线段BE,DC的中点.(1)求证:GF∥平面ADE;
(2)求平面AEF与平面BEC所成锐二面角的余弦值.
分析 解法一:(1)取AE的中点H,连接HG,HD,通过证明四边形HGFD是平行四边形来证明GF∥DH,由线面平行的判定定理可得;
(2)以B为原点,分别以$\overrightarrow{BE},\overrightarrow{BQ},\overrightarrow{BA}$的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,可得平面BEC和平面AEF的法向量,由向量夹角的余弦值可得.
解法二:(1)如图,取AB中点M,连接MG,MF,通过证明平面GMF∥平面ADE来证明GF∥平面ADE;(2)同解法一.
解答 解法一:(1)如图,取AE的中点H,连接HG,HD,
∵G是BE的中点,∴GH∥AB,且GH=$\frac{1}{2}$AB,
又∵F是CD中点,四边形ABCD是矩形,
∴DF∥AB,且DF=$\frac{1}{2}$AB,即GH∥DF,且GH=DF,
∴四边形HGFD是平行四边形,∴GF∥DH,
又∵DH?平面ADE,GF?平面ADE,∴GF∥平面ADE.
(2)如图,在平面BEG内,过点B作BQ∥CE,
∵BE⊥EC,∴BQ⊥BE,
又∵AB⊥平面BEC,∴AB⊥BE,AB⊥BQ,
以B为原点,分别以$\overrightarrow{BE},\overrightarrow{BQ},\overrightarrow{BA}$的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,
则A(0,0,2),B(0,0,0),E(2,0,0),F(2,2,1)
∵AB⊥平面BEC,∴$\overrightarrow{BA}=(0,0,2)$为平面BEC的法向量,
设$\overrightarrow{n}$=(x,y,z)为平面AEF的法向量.又$\overrightarrow{AE}$=(2,0,-2),$\overrightarrow{AF}$=(2,2,-1)
由垂直关系可得$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AE}=2x-2z=0}\\{\overrightarrow{n}•\overrightarrow{AF}=2x+2y-z=0}\end{array}\right.$,取z=2可得$\overrightarrow n=(2,-1,2)$.
∴cos<$\overrightarrow{n}$,$\overrightarrow{BA}$>=$\frac{\overrightarrow{n}•\overrightarrow{BA}}{|\overrightarrow{n}||\overrightarrow{BA}|}$=$\frac{2}{3}$
∴平面AEF与平面BEC所成锐二面角的余弦值为$\frac{2}{3}$.
解法二:(1)如图,取AB中点M,连接MG,MF,
又G是BE的中点,可知GM∥AE,且GM=$\frac{1}{2}$AE
又AE?平面ADE,GM?平面ADE,
∴GM∥平面ADE.
在矩形ABCD中,由M,F分别是AB,CD的中点可得MF∥AD.
又AD?平面ADE,MF?平面ADE,∴MF∥平面ADE.
又∵GM∩MF=M,GM?平面GMF,MF?平面GMF
∴平面GMF∥平面ADE,
∵GF?平面GMF,∴GF∥平面ADE
(2)同解法一.
点评 本题考查空间线面位置关系,考查空间想象能力、推理论证能力、运算求解能力,建系求二面角是解决问题的关键,属难题.

 阶梯计算系列答案
阶梯计算系列答案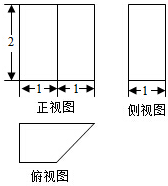
| A. | 8+2$\sqrt{2}$ | B. | 11+2$\sqrt{2}$ | C. | 14+2$\sqrt{2}$ | D. | 15 |
| A. | $-\frac{5}{2}$ | B. | -2 | C. | $-\frac{3}{2}$ | D. | 2 |