题目内容
11．若锐角△ABC的面积为$10\sqrt{3}$，且AB=5，AC=8，则BC等于7．分析 利用三角形的面积公式求出A，再利用余弦定理求出BC．
解答 解：因为锐角△ABC的面积为$10\sqrt{3}$，且AB=5，AC=8，
所以$\frac{1}{2}×5×8×sinA=10\sqrt{3}$，
所以sinA=$\frac{\sqrt{3}}{2}$，
所以A=60°，
所以cosA=$\frac{1}{2}$，
所以BC=$\sqrt{{5}^{2}+{8}^{2}-2×5×8×\frac{1}{2}}$=7．
故答案为：7．
点评 本题考查三角形的面积公式，考查余弦定理的运用，比较基础．
练习册系列答案
相关题目
1．执行如图所示的程序框图，则输出s的值为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{5}{6}$ | C． | $\frac{11}{12}$ | D． | $\frac{25}{24}$ |
2．阅读如图所示的程序框图，运行相应的程序，若输入x的值为1，则输出y的值为（ ）
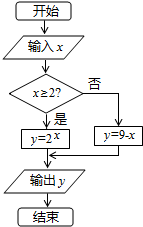
| A． | 2 | B． | 7 | C． | 8 | D． | 128 |
6．若l，m是两条不同的直线，m垂直于平面α，则“l⊥m”是“l∥α”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
线段BE，DC的中点．
3．i为虚数单位，i607的共轭复数为（ ）
| A． | i | B． | -i | C． | 1 | D． | -1 |
20．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一个焦点为F（2，0），且双曲线的渐近线与圆（x-2）2+y2=3相切，则双曲线的方程为（ ）
| A． | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{13}$=1 | B． | $\frac{{x}^{2}}{13}$-$\frac{{y}^{2}}{9}$=1 | C． | $\frac{{x}^{2}}{3}$-y2=1 | D． | x2-$\frac{{y}^{2}}{3}$=1 |