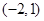题目内容
已知函数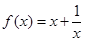
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明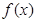 在
在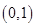 上是减函数;
上是减函数;
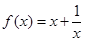
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明
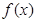 在
在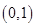 上是减函数;
上是减函数;(1)见解析(1)
(2)见解析(2)
(2)见解析(2)
(1)因为f(-x)=-f(x),所以函数f(x)为奇函数.
证明:函数为奇函数,函数定义域为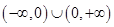 ……………1分
……………1分
∵ ………………3分
………………3分
∴函数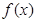 为奇函数………………4分
为奇函数………………4分
(2)利用单调性的定义可在(0,1)内任取两个不同的值,然后再采用作差比较的方法求出两个函数值的大小,分解因式后再分别判别每个因式的符号,最终确定差值的符号.
设 且
且 ………………5分
………………5分
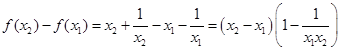
 ………9分
………9分
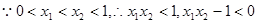
 .
.
 ………………11分
………………11分
因此函数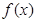 在
在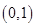 上是减函数………………12分
上是减函数………………12分
证明:函数为奇函数,函数定义域为
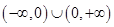 ……………1分
……………1分∵
 ………………3分
………………3分∴函数
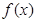 为奇函数………………4分
为奇函数………………4分(2)利用单调性的定义可在(0,1)内任取两个不同的值,然后再采用作差比较的方法求出两个函数值的大小,分解因式后再分别判别每个因式的符号,最终确定差值的符号.
设
 且
且 ………………5分
………………5分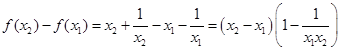
 ………9分
………9分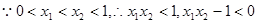
 .
. ………………11分
………………11分因此函数
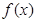 在
在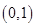 上是减函数………………12分
上是减函数………………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
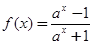 ,其中
,其中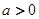 且
且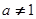 .
.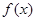 的奇偶性;
的奇偶性;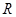 上的单调性,并加以证明.
上的单调性,并加以证明.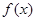 为二次函数,-1和3是方程
为二次函数,-1和3是方程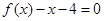 的两根,
的两根,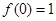
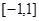 上,不等式
上,不等式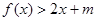 有解,求实数m的取值范围。
有解,求实数m的取值范围。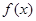 是定义在
是定义在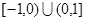 上的偶函数,当
上的偶函数,当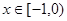 时,
时,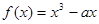 (
(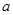 是实数)。
是实数)。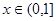 时,求f(x)的解析式;
时,求f(x)的解析式;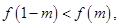 求实数m的取值范围.
求实数m的取值范围.
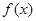 是定义在(0,+∞)上的单调增函数,满足:
是定义在(0,+∞)上的单调增函数,满足: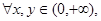 恒有
恒有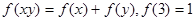 ,求:
,求: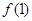 ;
;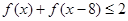 ,求
,求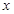 的取值范围。
的取值范围。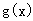 是
是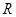 上的奇函数,且当
上的奇函数,且当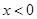 时
时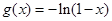 ,
,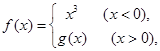 若
若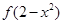 >
>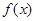 ,则实数
,则实数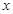 的取值范围是
的取值范围是