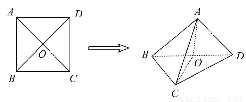
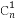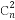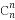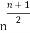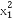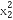题目内容
已知函数f(x)是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足:f(a·b)=af(b)+bf(a),f(2)=2,an=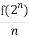 (n∈N*),bn=
(n∈N*),bn=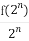 (n∈N*).
(n∈N*).
考察下列结论:
①f(0)=f(1);②f(x)为偶函数;
③数列{an}为等比数列;
④数列{bn}为等差数列.
其中正确的结论共有( )
(A)1个 (B)2个 (C)3个 (D)4个
C
【解析】根据所给的四个条件,逐条验证即可.注意②中用特殊值验证,③④用定义判断.
∵f(0)=f(0×0)=0,
f(1)=f(1×1)=2f(1),
∴f(1)=0,①正确;
又f(1)=f((-1)×(-1))=-2f(-1),
∴f(-1)=0,f(-2)=f(-1×2)=-f(2)+2f(-1)=-2≠f(2),
故f(x)不是偶函数,故②错;
∵f(2n)=f(2·2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,
∴ =
=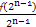 +1,
+1,
即bn=bn-1+1,
∴{bn}是等差数列,④正确;
b1=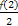 =1,
=1,
bn=1+(n-1)·1=n,
f(2n)=2nbn=n·2n,
an=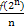 =2n,
=2n,
故数列{an}是等比数列,③正确.故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目