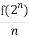Question

如果a<0,b<0,则必有(　　)

(A)a3+b3≥ab2+a2b (B)a3+b3≤ab2+a2b

(C)a3+b3>ab2+a2b (D)a3+b3<ab2+a2b

 

Answer 1

B

【解析】(a3+b3)-(ab2+a2b)

=(a3-ab2)-(a2b-b3)

=a(a2-b2)-b(a2-b2)

=(a2-b2)(a-b)

=(a-b)2(a+b),

由于a<0,b<0,所以(a-b)2≥0,a+b<0,

于是(a3+b3)-(ab2+a2b)≤0,

故a3+b3≤ab2+a2b.