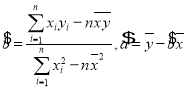题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的焦点且垂直于
的焦点且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
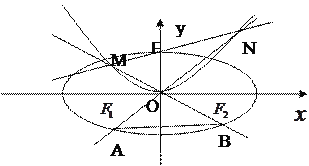
(2)设点![]() 均在椭圆
均在椭圆![]() 上,点
上,点![]() 在抛物线
在抛物线![]() 上,若
上,若![]() 的重心为坐标原点
的重心为坐标原点![]() ,且
,且![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2) ,或
,或![]() .
.
【解析】
(1)运用离心率公式和垂直于![]() 轴的弦长公式,以及
轴的弦长公式,以及![]() 的关系解方程可得
的关系解方程可得![]() ,进而得到所求椭圆的方程;
,进而得到所求椭圆的方程;
(2)设![]() ,联立椭圆方程,运用韦达定理和中点坐标公式、三角形的重心坐标公式,可得
,联立椭圆方程,运用韦达定理和中点坐标公式、三角形的重心坐标公式,可得![]() 的坐标,代入抛物线方程,结合三角形的面积公式,计算可得
的坐标,代入抛物线方程,结合三角形的面积公式,计算可得![]() 的坐标.
的坐标.
(1)根据题意得 ,又因为
,又因为![]() ,解得
,解得![]() ,则
,则![]() ,
,
所以椭圆![]() 的方程为:
的方程为:![]() ;
;
(2)设![]() ,联立椭圆方程
,联立椭圆方程![]() ,可得
,可得![]() ,
,
![]() ①
①
设![]() ,
,![]() ,
,
可得![]() ,
,
![]() ,
,
由![]() 在抛物线
在抛物线![]() 上,可得
上,可得![]() ,
,
则![]() ②
②![]() ,
,
由![]()
![]()
![]() ,
,
则![]()
 ,
,
可得 ③,将②代入③整理可得
③,将②代入③整理可得![]() ,
,
解得![]() 或
或![]() ,相应的
,相应的![]() 或1.
或1.
所以 ,或
,或![]() .
.

练习册系列答案
相关题目
【题目】某省的一个气象站观测点在连续4天里记录的AQI指数M与当天的空气水平可见度y(单位:cm)的情况如下表:
M | 900 | 700 | 300 | 100 |
y | 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2019年12月份AQI指数M的频数分布表如下:
M |
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,若x与y之间具有线性关系,试根据上述数据求出y关于x的线性回归方程;
,若x与y之间具有线性关系,试根据上述数据求出y关于x的线性回归方程;
(2)王先生在该市开了一家洗车店,洗车店每天的平均收入与AQI指数的相关关系如下表:
M |
|
|
|
|
|
日均收入(元) | -2000 | -1000 | 2000 | 6000 | 8000 |
估计王先生的洗车店2019年12月份每天的平均收入.
附参考公式:![]() ,其中
,其中