Question

【题目】如果方程y|y|＝1所对应的曲线与函数y＝f（x）的图象完全重合，那么对于函数y＝f（x）有如下结论：

①函数f（x）在R上单调递减；

②y＝f（x）的图象上的点到坐标原点距离的最小值为1；

③函数f（x）的值域为（﹣∞，2]；

④函数F（x）＝f（x）+x有且只有一个零点.

其中正确结论的序号是_____.

Answer 1

【答案】②④

【解析】

由题意分类画出函数图象，结合函数图象逐一核对四个选项得答案.

当y≥0时，方程y|y|＝1化为（y≥0），

当y＜0时，方程y|y|＝1化为（y＜0）.

作出函数f（x）的图象如图：

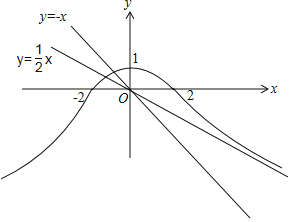
由图可知，函数f（x）在R上不是单调函数，故①错误；

y＝f（x）的图象上的点到坐标原点距离的最小值为1，故②正确；

函数f（x）的值域为（﹣∞，1]，故③错误；

双曲线的渐近线方程为y，故函数y＝f（x）与y＝﹣x的图象只有1个交点，即函数F（x）＝f（x）+x有且只有一个零点，故④正确.

故答案为：②④.