题目内容
9.f(x)=ax3+bx2-3x在x=-1处的极大值2.(1)求f(x)的解析式;
(2)若过点A(1,m)(m≠2)可作曲线的三条切线,求m的取值范围.
分析 (1)由f(x)=ax3+bx2-3x在x=-1处取得极大值2,建立方程关系求解即可;
(2)由题意知,点A不在曲线上,故设出切点为M(x0,y0),根据切点在曲线y=f(x)上和导数的几何意义建立等量关系,推出2x03-3x02+m+3=0,由题意知,该方程有3个解,故将问题转化为g(x0)=2x03-3x02+m+3的极大值和极小值异号的问题,从而求出实数m的取值范围.
解答 解:(1)f′(x)=3ax2+2bx-3,
∵在x=-1处的极大值2,
∴f′(-1)=0,且f(-1)=2,
则3a-2b-3=0且-a+b+3=2,
解得a=1,b=0.
∴f(x)=x3-3x.
(2)f′(x)=3x2-3=3(x+1)(x-1),
∵曲线方程为y=x3-3x,
∴点A(1,m)不在曲线上.
设切点为M(x0,y0),则点M的坐标满足y0=x03-3x0.
∵f′(x0)=3(x02-1),
∴切线的斜率为$3(x_0^2-1)=\frac{{x_0^3-3{x_0}-m}}{{{x_0}-1}}$,
整理得2x03-3x02+m+3=0.
∵过点A(1,m)可作曲线的三条切线,
∴关于x0方程2x03-3x02+m+3=0有三个实根.
设g(x0)=2x03-3x02+m+3,
则g′(x0)=6x02-6x0,
由g′(x0)=0,得x0=0或x0=1.
∴函数g(x0)=2x03-3x02+m+3的极值点为x0=0,x0=1.
∴关于x0方程2x03-3x02+m+3=0有三个实根的充要条件是g(1)g(0)<0,
即(m+3)(m+2)<0,解得-3<m<-2.
故所求的实数a的取值范围是-3<m<-2.
点评 本题考查了导数的几何意义,利用导数求函数的极值和最值等知识,考查学生的计算能力,综合性较强,难度较大.

| A. | {x|-1<x≤0} | B. | {x|0≤x<1} | C. | {x|-1<x≤0,或x=1} | D. | {x|0≤x<1,或x=-1} |
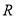 的函数
的函数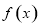 满足下列条件:①对任意的实数
满足下列条件:①对任意的实数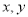 都有:
都有: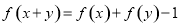 ;②当
;②当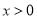 时,
时,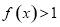 .
.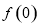 ;
;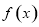 在
在 上为增函数;
上为增函数;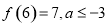 ,关于
,关于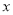 的不等式
的不等式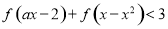 对任意
对任意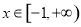 恒成立,求实数
恒成立,求实数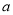 的取值范围.
的取值范围.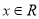 ,则“
,则“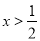 ”是“
”是“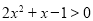 ”的( )
”的( )