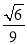题目内容
1.函数f(x)=x+$\frac{a}{x}$(a>0)在(0,$\sqrt{a}$)与($\sqrt{a}$,+∞)上是增函数还是减函数?请证明你的结论,并利用函数奇偶性与单调性关系,判断在(-$\sqrt{a}$,0)与(-∞,-$\sqrt{a}$)上的单调性.分析 根据函数单调性的定义,利用定义法进行证明即可.
解答 解:设x1<x2,
则f(x1)-f(x2)=x1+$\frac{a}{{x}_{1}}$-x2-$\frac{a}{{x}_{2}}$=(x1-x2)+$\frac{a({x}_{2}-{x}_{1})}{{x}_{1}{x}_{2}}$=(x1-x2)(1-$\frac{a}{{x}_{1}{x}_{2}}$)=(x1-x2)•$\frac{{x}_{1}{x}_{2}-a}{{x}_{1}{x}_{2}}$,
若0<x1<x2<$\sqrt{a}$,则x1-x2<0,0<x1x2<a,
即x1x2-a<0,则f(x1)-f(x2)>0,即f(x1)>f(x2),即在(0,$\sqrt{a}$)上是减函数.
若$\sqrt{a}$<x1<x2,则x1-x2<0,x1x2>a,
即x1x2-a>0,则f(x1)-f(x2)<0,即f(x1)<f(x2),即在($\sqrt{a}$,+∞)上是增函数.
∵f(-x)=-x-$\frac{a}{x}$=-(x+$\frac{a}{x}$)=-f(x),
∴f(x)是奇函数,
则在(-$\sqrt{a}$,0)上为减函数,在(-∞,-$\sqrt{a}$)上为增函数.
点评 本题主要考查函数单调性的判断和证明,利用函数单调性的定义是解决本题的关键.

练习册系列答案
相关题目
6.数列{an}满足a1=1,an+1=an+n+1(n∈N•),则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2015}}$等于( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{4028}{2015}$ | C. | $\frac{2015}{1008}$ | D. | $\frac{1007}{1008}$ |
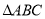 中,角
中,角 所对的边分别为
所对的边分别为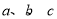 ,若
,若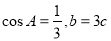 ,则
,则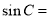 ( )
( )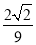 B.
B.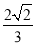 C.
C.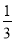 D.
D.