题目内容
(本题满分14分)设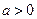 ,函数
,函数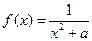 .
.
(Ⅰ)证明:存在唯一实数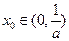 ,使
,使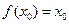 ;
;
(Ⅱ)定 义数列
义数列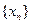 :
: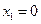 ,
,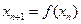 ,
,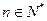 .
.
(i)求证:对任意正整数n都有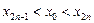 ;
;
(ii) 当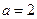 时,若
时,若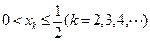 ,
,
证明:当k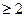 时,对任意
时,对任意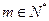 都有:
都有: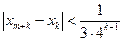
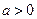 ,函数
,函数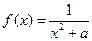 .
.(Ⅰ)证明:存在唯一实数
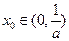 ,使
,使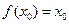 ;
;(Ⅱ)定
 义数列
义数列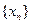 :
: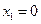 ,
,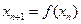 ,
,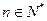 .
.(i)求证:对任意正整数n都有
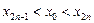 ;
;(ii) 当
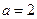 时,若
时,若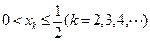 ,
,证明:当k
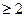 时,对任意
时,对任意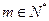 都有:
都有: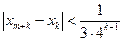
(Ⅰ)证明:略
(Ⅰ)证明: ① . ………1分
. ………1分
令 ,则
,则 ,
, ,
,
∴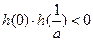 . ………………………………… 2分
. ………………………………… 2分
又 ,∴
,∴ 是R上的增函数. …………………… 3分
是R上的增函数. …………………… 3分
故 在区间
在区间 上有唯一零点,
上有唯一零点,
即存在唯一实数 使
使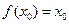 . ………………………………… 4分
. ………………………………… 4分
②当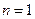 时,
时,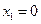 ,
,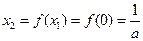 ,由①知
,由①知 ,即
,即
 成立;…… 5分
成立;…… 5分
设当 时,
时, ,注意到
,注意到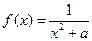 在
在 上是减函数,且
上是减函数,且 ,
,
故有: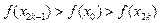 ,即
,即
∴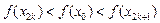 ,
,  ………………………………… 7分
………………………………… 7分
即 .这就是说,
.这就是说,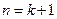 时
时 ,结论也成立.
,结论也成立.
故对任意正整数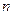 都有:
都有: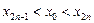 . ………………………………… 8分
. ………………………………… 8分
(2)当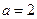 时,由
时,由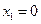 得:
得: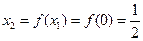 ,
,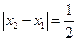 ……………… 9分
……………… 9分
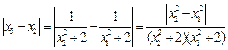
 ………10分
………10分
当 时,
时, ,
,
∴
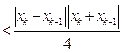


 ………………………………… 12分
………………………………… 12分
对 ,
,
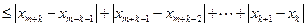 …………………
………………… ……………… 13分
……………… 13分
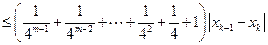

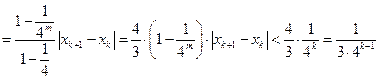 ………………… 14分
………………… 14分
 . ………1分
. ………1分令
 ,则
,则 ,
, ,
,∴
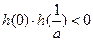 . ………………………………… 2分
. ………………………………… 2分又
 ,∴
,∴ 是R上的增函数. …………………… 3分
是R上的增函数. …………………… 3分故
 在区间
在区间 上有唯一零点,
上有唯一零点,即存在唯一实数
 使
使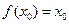 . ………………………………… 4分
. ………………………………… 4分②当
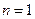 时,
时,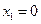 ,
,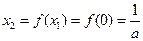 ,由①知
,由①知 ,即
,即
 成立;…… 5分
成立;…… 5分设当
 时,
时, ,注意到
,注意到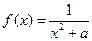 在
在 上是减函数,且
上是减函数,且 ,
,故有:
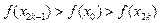 ,即
,即
∴
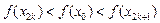 ,
,  ………………………………… 7分
………………………………… 7分即
 .这就是说,
.这就是说,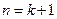 时
时 ,结论也成立.
,结论也成立.故对任意正整数
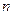 都有:
都有: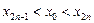 . ………………………………… 8分
. ………………………………… 8分(2)当
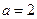 时,由
时,由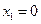 得:
得: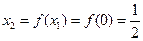 ,
,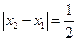 ……………… 9分
……………… 9分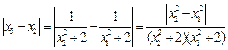
 ………10分
………10分当
 时,
时, ,
,∴

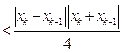


 ………………………………… 12分
………………………………… 12分对
 ,
,
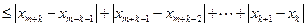 …………………
………………… ……………… 13分
……………… 13分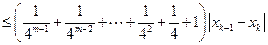

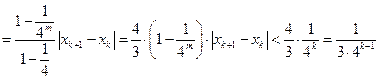 ………………… 14分
………………… 14分
练习册系列答案
相关题目
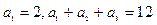
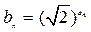 ,求数列{bn}的前10项和
,求数列{bn}的前10项和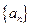 满足
满足 ,则
,则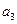 等于
等于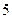
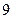
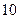
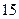
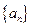 中,
中, ,
,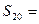
 是等差数列,且
是等差数列,且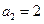 ,
, ,则该数列的通项公式
,则该数列的通项公式 __ ▲ __.
__ ▲ __.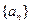 中,
中,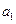 =1,
=1,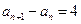 ,则
,则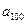 的值为 ★ .
的值为 ★ .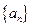 的前
的前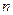 项和为
项和为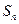 ,若
,若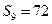 ,则
,则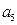 = ▲
= ▲ 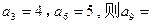
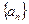 的前3项和
的前3项和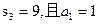 ,则
,则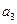 等于
等于