题目内容
6.设集合A={1,2,3,4,5},B={x|(x-1)(x-4)<0},则A∩B=( )| A. | {1,2,3,4} | B. | {2,3} | C. | {1,2,3} | D. | {2,3,4} |
分析 求出集合B,然后求解集合的交集即可.
解答 解:集合A={1,2,3,4,5},B={x|(x-1)(x-4)<0}={x|1<x<4},
∴A∩B={2,3}.
故选:B.
点评 本题考查集合的交集的求法,二次不等式的解法,考查计算能力.

练习册系列答案
相关题目
1.已知|$\overrightarrow{a}$|=2,$\overrightarrow{b}$为单位向量,$\overrightarrow{a}•\overrightarrow{b}$=1,则向量$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影是( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
18. 下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )
下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )
(注:标准差s=$\sqrt{\frac{1}{n}[{{({x_1}-\overline x)}^2}+{{({x_2}-\overline x)}^2}+…+{{({x_n}-\overline x)}^2}}$,其中$\overline{x_1}$为x1,x2,…,xn的平均数)
 下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )
下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )(注:标准差s=$\sqrt{\frac{1}{n}[{{({x_1}-\overline x)}^2}+{{({x_2}-\overline x)}^2}+…+{{({x_n}-\overline x)}^2}}$,其中$\overline{x_1}$为x1,x2,…,xn的平均数)
| A. | $\overline{x_1}$<$\overline{x_2}$,s1<s2 | B. | $\overline{x_1}$<$\overline{x_2}$,s1>s2 | C. | $\overline{x_1}$>$\overline{x_2}$,s1>s2 | D. | $\overline{x_1}$>$\overline{x_2}$,s1<s2 |
16.若二项式(2x+$\frac{a}{x}$)7的展开式中$\frac{1}{{x}^{3}}$项的系数是84,则实数a=( )
| A. | 2 | B. | $\root{3}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | 1 |
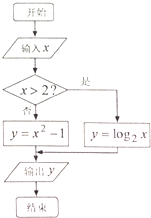 某函数的解析式由如图所示的程序框图给出.
某函数的解析式由如图所示的程序框图给出.