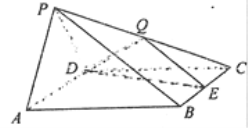
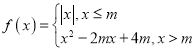题目内容
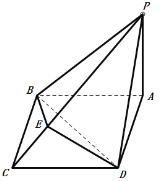
【题目】如图,已知动直线![]() 交圆
交圆![]() 于坐标原点
于坐标原点![]() 和点
和点![]() ,交直线
,交直线![]() 于点
于点![]() ;
;
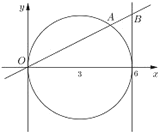
(1)若![]() ,求点
,求点![]() 、点
、点![]() 的坐标;
的坐标;
(2)设动点![]() 满足
满足![]() ,其轨迹为曲线
,其轨迹为曲线![]() ,求曲线
,求曲线![]() 的方程
的方程![]() ;
;
(3)请指出曲线![]() 的对称性、顶点和图形范围,并说明理由;
的对称性、顶点和图形范围,并说明理由;
(4)判断曲线![]() 是否存在渐近线,若存在,请直接写出渐近线方程;若不存在,说明理由.
是否存在渐近线,若存在,请直接写出渐近线方程;若不存在,说明理由.
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)曲线
(3)曲线![]() 关于
关于![]() 轴对称,曲线
轴对称,曲线![]() 的顶点为
的顶点为![]() ;图形范围满足
;图形范围满足![]() ,理由见解析(4)存在,
,理由见解析(4)存在,![]()
【解析】
(1)已知可得![]() 点的横坐标为6,结合
点的横坐标为6,结合![]() ,求出
,求出![]() 坐标,进而求出直线
坐标,进而求出直线![]() 方程,与圆方程联立,即可求出点
方程,与圆方程联立,即可求出点![]() 坐标;
坐标;
(2)设![]() 所在直线方程为
所在直线方程为![]() ,与圆方程联立,求出含有
,与圆方程联立,求出含有![]() 的
的![]() 两点坐标,设
两点坐标,设![]() ,
,![]() ,将向量用坐标表示,求出曲线
,将向量用坐标表示,求出曲线![]() 以
以![]() 为参数的方程,消去
为参数的方程,消去![]() ,即可求解;
,即可求解;
(3)由(2)曲线![]() 方程为
方程为![]() ,取
,取![]() 为
为![]() ,方程不变,可判断曲线
,方程不变,可判断曲线![]() 对称性;再由
对称性;再由![]() ,求出
,求出![]() 的取值范围,
的取值范围,![]() ,
,![]() ,求出定点坐标;
,求出定点坐标;
(4)由![]() 的范围,结合分式变化趋势,可确定渐近线方程.
的范围,结合分式变化趋势,可确定渐近线方程.
(1)由已知可得![]() 点的横坐标为6,则纵坐标为
点的横坐标为6,则纵坐标为![]() ,
,
设直线![]() 为
为![]() ,把
,把![]() 点坐标代入得
点坐标代入得![]() 则
则![]() ,
,
联立 ,
,
解得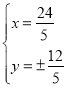 .
.
∴![]() ,
,![]() .
.
(2)设![]() 所在直线方程为
所在直线方程为![]() ,
,
联立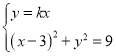 ,得
,得![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
∴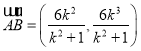 ,
,
设![]() ,则
,则 ,消去
,消去![]() 得:
得:![]() ;
;
(3)取![]() 为
为![]() ,曲线方程不变,∴曲线
,曲线方程不变,∴曲线![]() 关于
关于![]() 轴对称;
轴对称;
由![]() ,解得:
,解得:![]() ,
,
∴曲线![]() 的顶点为
的顶点为![]() ;图形范围满足
;图形范围满足![]() ;
;
(4)当![]() 时,若
时,若![]() ,则
,则![]() ,
,
∴曲线![]() 的渐近线方程为
的渐近线方程为![]() .
.

练习册系列答案
相关题目