题目内容
【题目】设数列
的前
项和为
，点
均在函数
的图象上.
(1)求证：数列为等差数列；
(2)设
是数列
的前
项和，求使
对所有
都成立的最小正整数
.
【答案】(1)详见解析(2)10
【解析】
试题分析：(1)由题意得到关系式
，由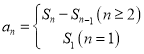
可求得数列通项公式，从而证明数列为等差数列；(2) 首先整理
的通项公式
＝
，依据特点采用裂项相消法求和可求得
，从而得到最小正整数
试题解析：(1)依题意，
＝3n－2，即Sn＝3n2－2n，…………………1分
n≥2时，an＝Sn－Sn－1＝(3n2－2n)－[3(n－1)2－2(n－1)]
＝6n－5. ……………………………………………3分
当n＝1时，a1＝S1＝1符合上式，…………………………4分
所以an＝6n－5(n∈N＋).…………………………5分
又∵an－an－1＝6n－5－[6(n－1)－5]＝6，
∴{an}是一个以1为首项，6为公差的等差数列.…………………………6分
(2)由(1)知，
＝＝
…………………………8分
故Tn＝
[(1－
)＋(
－
)＋…＋(
－
)]＝
(1－
)，………10分
因此使得
(1－
)<
(n∈N＋)成立的m必须且仅需满足
≤
，
即m≥10，故满足要求的最小正整数m为10.…………………………12分
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温度与实验室每天每100颗种子中的发芽数，得到如下数据：
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是：先从这5组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验．
（Ⅰ）求选取的2组数据恰好是不相邻的2天数据的概率；
（Ⅱ）若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求
关于
的线性回归方程
；
（Ⅲ）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（Ⅱ）中所得的线性回归方程是否可靠？
（注：
）
