题目内容
【题目】命题p:方程![]() 没有实数根(
没有实数根(![]() ),命题q:
),命题q:![]() 定义域为R,若命题p
定义域为R,若命题p![]() 为真命题,p
为真命题,p ![]() 为假命题,求k的取值范围
为假命题,求k的取值范围
【答案】(-3,0)∪[3,4)
【解析】
试题分析:首先求解命题p,q为真命题时的对应的k的取值范围,由命题p![]() 为真命题,p
为真命题,p ![]() 为假命题可知两命题一真一假,分情况讨论可得到k的取值范围
为假命题可知两命题一真一假,分情况讨论可得到k的取值范围
试题解析:命题q:方程![]() 没有实数根(
没有实数根(![]() ),
),
![]() =
=![]() <0,
<0,![]() <k<3-----------2分
<k<3-----------2分
命题q:g(x)=![]() 恒成立,………………………..3分
恒成立,………………………..3分
当k=0时;1>0恒成立,符合条件…………………………….4分
当k![]() 时;
时;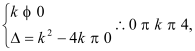 综上.
综上.![]() …………….6分
…………….6分
命题p![]() 为真命题,p
为真命题,p ![]() 为假命题,则p,q一真一假………………………………7分
为假命题,则p,q一真一假………………………………7分
如果p真且q假,则 ………………………..9分
………………………..9分
如果p假且q真,则
![]() …………………………….11分
…………………………….11分
综上,k的取值范围为(-3,0)∪[3,4).…………………………………….12分

【题目】为了了解我校高2017级本部和大学城校区的学生是否愿意参加自主招生培训的情况,对全年级2000名高三学生进行了问卷调查,统计结果如下表:
校区 | 愿意参加 | 不愿意参加 |
重庆一中本部校区 | 220 | 980 |
重庆一中大学城校区 | 80 | 720 |
(1)若从愿意参加自主招生培训的同学中按分层抽样的方法抽取15人,则大学城校区应抽取几人;
(2)现对愿意参加自主招生的同学组织摸底考试,考试题共有5道题,每题20分,对于这5道题,考生“如花姐”完全会答的有3题,不完全会的有2道,不完全会的每道题她得分![]() 的概率满足:
的概率满足:![]() ,假设解答各题之间没有影响,
,假设解答各题之间没有影响,
①对于一道不完全会的题,求“如花姐”得分的均值![]() ;
;
②试求“如花姐”在本次摸底考试中总得分的数学期望.
【题目】某城市随机抽取一年(365天)内100天的空气质量指数![]() 的检测数据,结果统计如下:
的检测数据,结果统计如下:
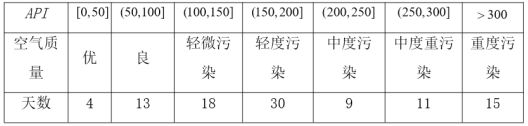
记某企业每天由空气污染造成的经济损失![]() (单位:元),空气质量指数
(单位:元),空气质量指数![]() 为
为![]() .在区间
.在区间![]() 对企业没有造成经济损失;在区间
对企业没有造成经济损失;在区间![]() 对企业造成经济损失成直线模型(当
对企业造成经济损失成直线模型(当![]() 为150时造成的经济损失为500元,当
为150时造成的经济损失为500元,当![]() 为200时,造成的经济损失为700元);当
为200时,造成的经济损失为700元);当![]() 大于300时造成的经济损失为2000元.
大于300时造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失![]() 大于200元且不超过600元的概率;
大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面![]() 列联表,并判断
列联表,并判断
能否有![]() 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.82 |
![]()
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |