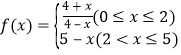Question

【题目】设数列是首项为0的递增数列，，满足：对于任意的总有两个不同的根，则的通项公式为_________

Answer 1

【答案】

【解析】

试题分析：∵，当n=1时，f1（x）=|sin（x-a1）|=|sinx|，x∈[0，a2]，

又∵对任意的b∈[0，1），f1（x）=b总有两个不同的根，∴a2=π

∴f1（x）=sinx，x∈[0，π]，a2=π

又f2（x）=|sin （x-a2）|=|sin （x-π）|=|cos |，x∈[π，a3]

∵对任意的b∈[0，1），f1（x）=b总有两个不同的根，∴…（5分）

又f3（x）=|sin （x-a3）|=|sin （x-3π）|=|sin π|，x∈[3π，a4]

∵对任意的b∈[0，1），f1（x）=b总有两个不同的根，∴a4=6π…（6分）

由此可得，

∴

∴