题目内容
选修4-5：不等式选讲
设函数f（x）=|2x-4|+|x+2|
（Ⅰ）求函数y=f（x）的最小值；
（Ⅱ）若不等式f（x）≥|a+4|-|a-3|恒成立，求a的取值范围．
设函数f（x）=|2x-4|+|x+2|
（Ⅰ）求函数y=f（x）的最小值；
（Ⅱ）若不等式f（x）≥|a+4|-|a-3|恒成立，求a的取值范围．
（Ⅰ）由于f（x）=|2x-4|+|x+2|=
可得当x＜-2时，-3x+2＞8，当-2≤x＜2时，4＜6-x≤8，
当x≥2时，3x-2≥4，
所以函数的最小值为f（2）=4．
（Ⅱ）若不等式f（x）≥|a+4|-|a-3|恒成立，则|a+4|-|a-3|≤f（x）min=4，
又解不等式|a+4|-|a-3|≤4可解得a≤
．所以a的取值范围为a≤
|
可得当x＜-2时，-3x+2＞8，当-2≤x＜2时，4＜6-x≤8，
当x≥2时，3x-2≥4，
所以函数的最小值为f（2）=4．
（Ⅱ）若不等式f（x）≥|a+4|-|a-3|恒成立，则|a+4|-|a-3|≤f（x）min=4，
又解不等式|a+4|-|a-3|≤4可解得a≤
| 3 |
| 2 |
| 3 |
| 2 |
练习册系列答案
相关题目
的解集为 .
表示
，
两者中的较小的一个，若函数
，则满足
的
的集合为 （ ）
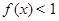的解集为 ( )
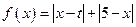的最小值为3, 
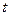的值是________.