题目内容
【题目】某工厂拟造一座平面为长方形,面积为![]() 的三级污水处理池.由于地形限制,长、宽都不能超过
的三级污水处理池.由于地形限制,长、宽都不能超过![]() ,处理池的高度一定.如果池的四周墙壁的造价为
,处理池的高度一定.如果池的四周墙壁的造价为![]() 元
元![]() ,中间两道隔墙的造价为
,中间两道隔墙的造价为![]() 元
元![]() ,池底的造价为
,池底的造价为![]() 元
元![]() ,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元?
,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元?
【答案】![]() ,
,![]() .
.
【解析】试题分析:应用问题首先要认真细致的审题,逐字逐句的读题,把实际问题转化为数学问题.首先根据提议设出未知数,根据各项造价表示出总造价建立函数模型,根据实际需要写出函数的定义域,由于![]() ,借助a,b关系进行减元,化为只含有a的函数关系,再利用均值不等式求最值.
,借助a,b关系进行减元,化为只含有a的函数关系,再利用均值不等式求最值.
试题解析:
设污水处理水池的长、宽分别为![]() ,总造价为y元,
,总造价为y元,
则![]() ,
,
![]()
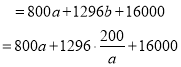 ,
, ![]()
易知函数是减函数,所以当![]() 时总造价最低,
时总造价最低,
最低造价为45000元.

练习册系列答案
相关题目

