题目内容
【题目】函数![]() 的定义域为
的定义域为![]() ,对给定的正数
,对给定的正数![]() ,若存在闭区间
,若存在闭区间![]() ,使得函数
,使得函数![]() 满足:①
满足:①![]() 在
在![]() 内是单调函数;②
内是单调函数;②![]() 在
在![]() 上的值域为
上的值域为![]() ,则称区间
,则称区间![]() 为
为![]() 的
的![]() 级“理想区间”.下列结论错误的是( )
级“理想区间”.下列结论错误的是( )
A. 函数![]() (
(![]() )存在1级“理想区间”
)存在1级“理想区间”
B. 函数![]() (
(![]() )不存在2级“理想区间”
)不存在2级“理想区间”
C. 函数![]() (
(![]() )存在3级“理想区间”
)存在3级“理想区间”
D. 函数![]() ,
, ![]() 不存在4级“理想区间”
不存在4级“理想区间”
【答案】D
【解析】A中,当x0时,f(x)=x2在[0,1]上是单调增函数,且f(x)在[0,1]上的值域是[0,1],
∴存在1级“理想区间”,原命题正确;
B中,当x∈R时,f(x)=ex在[a,b]上是单调增函数,且f(x)在[a,b]上的值域是[ea,eb],
∴不存在2级“理想区间”,原命题正确;
C中,因为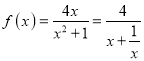 在(0,1)上为增函数。
在(0,1)上为增函数。
假设存在[a,b](0,1),使得f(x)∈[3a,3b]则有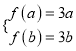 ,所以命题正确;
,所以命题正确;
D中,不妨设a>1,则函数在定义域内为单调增函数,
若存在“4级理想区间”[m,n],
则由m,n是方程tanx=4x,x∈![]() 的两个根,
的两个根,
由于该方程不存在两个不等的根,
故不存在“4级理想区间”[m,n],
∴D结论错误
本题选择D选项.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目