题目内容
【题目】已知等边三角形![]() 的边长为
的边长为![]() ,
,![]() 为
为![]() 边的中点,沿
边的中点,沿![]() 将
将![]() 折成直二面角
折成直二面角![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积为_____
的外接球的表面积为_____
【答案】![]()
【解析】
先证明AD⊥平面BCD,利用二面角的定义得知∠BDC=90°,利用勾股定理可得出△BCD的外接圆直径为BC,设R为三棱锥A﹣BCD的外接球的半径,得![]() ,再利用球体表面积公式可得出答案.
,再利用球体表面积公式可得出答案.
如图所示,
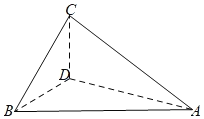
折叠前,由于△ABC时等边三角形,D为BC的中点,则AD⊥BC,
折叠后,则有AD⊥CD,AD⊥BD,∵BD∩CD=D,∴AD⊥平面BCD,
∵二面角B﹣AD﹣C为直二面角,∵AD⊥BD,AD⊥CD,则二面角B﹣AD﹣C的平面角为∠BDC=90°,
且![]() ,
,
Rt△BCD的外接圆直径为![]() ,
,
所以,三棱锥A﹣BCD的外接球半径为![]() ,
,
因此,三棱锥A﹣BCD的外接球的表面积为4πR2=80π.
故答案为:80π

练习册系列答案
相关题目