题目内容
1.设函数f(x)=x3-3ax+b(a≠0).(1)若曲线y=f(x)在点(2,f(2))处与直线y=8相切,求a,b的值;
(2)求函数f(x)的单调性与极值点.
分析 (1)求出原函数的导函数,由y=f(x)在点(2,f(x))处与直线y=8相切列关于a,b的方程组,解方程组求解a,b的值;
(2)求出原函数的导函数,由导函数大于0求解x的取值范围,得函数的增区间,由导函数小于0求解x的取值范围,得函数的减区间,从而得到函数的极值点.
解答 解:(1)由f(x)=x3-3ax+b(a≠0),得f′(x)=3x2-3a,
∵曲线y=f(x)在点(2,f(2))处与直线y=8相切
∴$\left\{\begin{array}{l}{f′(2)=0}\\{f(2)=8}\end{array}\right.$,∴$\left\{\begin{array}{l}{3(4-a)=0}\\{8-6a+b=8}\end{array}\right.$,
解得:a=4,b=24,
∴a=4,b=24;
(2)由f(x)=x3-3ax+b(a≠0),得f′(x)=3x2-3a,
当a<0时,f′(x)>0,函数f(x)为定义域上的增函数,函数f(x)不存在极值;
当a>0时,由3x2-3a>0,得x<-$\sqrt{a}$或x>$\sqrt{a}$,
由3x2-3a<0,得-$\sqrt{a}$<x<$\sqrt{a}$,
∴函数f(x)在(-∞.-$\sqrt{a}$),($\sqrt{a}$,+∞)上为增函数,在(-$\sqrt{a}$,$\sqrt{a}$)上为减函数.
∴x=-$\sqrt{a}$是f(x)的极大值点,x=$\sqrt{a}$是f(x)的极小值点.
点评 本题考查了利用导数研究曲线上某点处的切线方程,考查了利用导数研究函数的极值,考查了函数导函数的符号与原函数的单调性之间的关系,是中档题

练习册系列答案
相关题目
11.在下列四个函数中,在区间(0,$\frac{π}{2}$)上为增函数,且以π为最小正周期的偶函数是( )
| A. | y=tanx | B. | y=|sinx| | C. | y=sin2x | D. | y=cos2x |
16.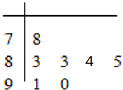 在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
 在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85和6.8 | B. | 85和1.6 | C. | 86和6.8 | D. | 86和1.6 |
13.设集合M={a2-a,0}.若a∈M,则实数a的值为( )
| A. | 0 | B. | 2 | C. | 2或0 | D. | 2或-2 |