题目内容
抛物线y2=2px（p＞0）上一点M（1，m） （m＞0）到其焦点的距离为5，双曲线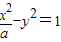
的左顶点为A．若双曲线的一条渐近线与直线AM平行，则实数a等于 ．
【答案】分析：由题意可求抛物线线y2=2px的准线，从而可求p，，进而可求M，由双曲线方程可求A，根据双曲线的一条渐近线与直线AM平行，则由斜率相等可求a
解答：解：由题意可知：抛物线线y2=2px（p＞0）的准线方程为x=-4
∴p=8
则点M（1，4），双曲线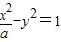
的左顶点为A（-
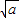，0），
所以直线AM的斜率为k=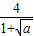
，
由题意可知：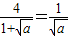
∴
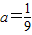
故答案为：
点评：本题主要考查了抛物线的性质的应用，双曲线的性质的应用，解题的关键是灵活利用抛物线的定义求出抛物线的准线方程．
解答：解：由题意可知：抛物线线y2=2px（p＞0）的准线方程为x=-4
∴p=8
则点M（1，4），双曲线
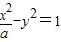的左顶点为A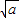（-，0），所以直线AM的斜率为k=
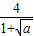，由题意可知：
∴
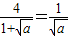
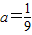
故答案为：
点评：本题主要考查了抛物线的性质的应用，双曲线的性质的应用，解题的关键是灵活利用抛物线的定义求出抛物线的准线方程．
练习册系列答案
阅读快车系列答案
相关题目
如图过抛物线y2=2px（p＞0）的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|=2|BF|，且|AF|=3，则抛物线的方程为（ ）A、y2=
| ||
| B、y2=9x | ||
C、y2=
| ||
| D、y2=3x |