Question

抛物线y²=2px，（p＞0）绕焦点依逆时针方向旋转90°所得抛物线方程为…（　　）

• A．x²=2py
• B．(x-

  p

  2

  )2=-2py
• C．(x-

  p

  2

  )2=2p(y+

  p

  2

  )
• D．(x-

  p

  2

  )2=-2p(y-

  p

  2

  )

Answer 1

分析：先根据题意画出旋转变换后的图形，如图，所得抛物线是虚线部分，其顶点A的坐标为（

p

2

，-

p

2

），开口向上，且与原来的抛物线全等，即可写出其方程．

解答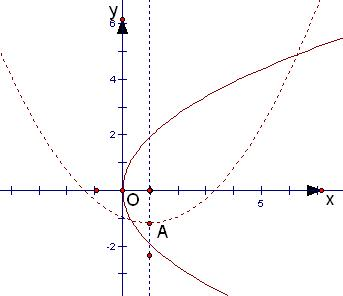：解：如图，抛物线y²=2px，（p＞0）绕焦点依逆时针方向旋转90°所得抛物线是虚线部分，其顶点A的坐标为（

p

2

，-

p

2

），开口向上，且与原来的抛物线全等，
故其方程为(x-

p

2

)2=2p(y+

p

2

)．
故选C．

点评：本题主要考查了旋转变换，考查了抛物线的方程，属于基础题．