题目内容
11．设f（n）=2+24+27+210+…+23n+1（n∈N），则f（n）等于（ ）| A． | $\frac{2}{7}$（8n-1） | B． | $\frac{2}{7}$（8n+1） | C． | $\frac{2}{7}$（8n+1-1） | D． | $\frac{2}{7}$（8n+1+1） |
分析 利用等比数列的前n项和公式即可得出．
解答 解：由题易知f（n）可看作是首项为2、公比为23=8的等比数列的前n+1项和，
∴f（n）=$\frac{2（1-{8}^{n+1}）}{1-8}$=$\frac{2（{8}^{n+1}-1）}{7}$，
故选：C．
点评 本题考查了等比数列的前n项和公式，属于基础题．
练习册系列答案
相关题目
1．若${（{{x^2}-\frac{1}{ax}}）^9}$（a∈R）的展开式中x9的系数是-$\frac{21}{2}$，则$\int_0^a{sinxdx}$的值为（ ）
| A． | 1-cos2 | B． | 2-cos1 | C． | cos2-1 | D． | 1+cos2 |
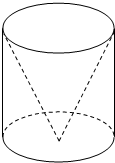如图所示，一圆柱内挖去一个圆锥，圆锥的顶点是圆柱底面的圆心，圆锥的底面是圆柱的另一个底面．圆柱的母线长为6，底面半径为2，求该几何体的表面积．