题目内容
【题目】已知数列{an}满足an+2= ![]() ,且a1=1,a2=2.
,且a1=1,a2=2.
(1)求a3﹣a6+a9﹣a12+a15的值;
(2)设数列{an}的前n项和为Sn , 当Sn>2017时,求n的最小值.
【答案】
(1)解:∵an+2= ![]() ,且a1=1,a2=2.
,且a1=1,a2=2.
∴a2n﹣1=1+2(n﹣1)=2n﹣1,a2n=2×3n﹣1,
∴a3﹣a6+a9﹣a12+a15=3a9﹣a6﹣a12=3×(2×9﹣1)﹣2×32﹣2×35=﹣477.
(2)解:由(1)可知:an>0,数列{an}单调递增.
S2n=(a1+a3+…+a2n﹣1)+(a2+a4+…+a2n)=n2+3n﹣1,
S12=62+36﹣1=764,S13=S12+a13=777,S14=72+37﹣1=2235.
∴当Sn>2017时,n的最小值为14.
【解析】(1)an+2= ![]() ,且a1=1,a2=2.可得a2n﹣1=2n﹣1,a2n=2×3n﹣1 , 即可得出:a3﹣a6+a9﹣a12+a15=3a9﹣a6﹣a12 . (2)由(1)可知:an>0,数列{an}单调递增.可得S2n=(a1+a3+…+a2n﹣1)+(a2+a4+…+a2n)=n2+3n﹣1, 分别求出S12 , S13 , S14 . 即可得出.
,且a1=1,a2=2.可得a2n﹣1=2n﹣1,a2n=2×3n﹣1 , 即可得出:a3﹣a6+a9﹣a12+a15=3a9﹣a6﹣a12 . (2)由(1)可知:an>0,数列{an}单调递增.可得S2n=(a1+a3+…+a2n﹣1)+(a2+a4+…+a2n)=n2+3n﹣1, 分别求出S12 , S13 , S14 . 即可得出.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系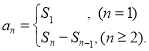 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

练习册系列答案
相关题目
