题目内容
已知 是公比为
是公比为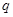 的等比数列,且
的等比数列,且 成等差数列.
成等差数列.
⑴求q的值;
⑵设 是以2为首项,
是以2为首项,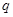 为公差的等差数列,其前
为公差的等差数列,其前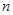 项和为
项和为 ,当n≥2时,比较
,当n≥2时,比较 与
与 的大小,并说明理由.
的大小,并说明理由.
(1) 或
或 (2)详见解析.
(2)详见解析.
解析试题分析:(1)等比数列中的等差数列问题,解题关键要根据题意列方程,该题可利用等差中项列方程,可得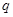 的值;(2)求出等差数列
的值;(2)求出等差数列 的前n项和
的前n项和 和通项公式
和通项公式 ,可以根据解析式的特点选择作商比较或者作差比较法,
,可以根据解析式的特点选择作商比较或者作差比较法,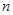 的范围要注意.
的范围要注意.
试题解析:(1)由题设 即
即

∴
 或
或 .
.
(2)若 则
则 ,
,
当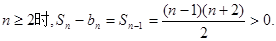 故
故
若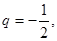 则
则 ,
,
当
故对于 ,当
,当 时,
时, ;当
;当 时,
时, ;当
;当 时,
时,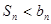 .
.
考点:1、等差数列的通项公式和前项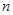 和;2、比较法;3、等比数列的通项公式.
和;2、比较法;3、等比数列的通项公式.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.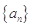 的前n项和为
的前n项和为 ,已知
,已知 ,
, 是
是 和
和 的等比中项.
的等比中项. 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有 (
( 为正常数).
为正常数). 满足
满足 ,
, ,求数列
,求数列 的前
的前 .
. 中,
中, (
( ).
). 的值;
的值; ,使得数列
,使得数列 是一个等差数列?若存在,求
是一个等差数列?若存在,求 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由. 满足
满足 ,
,
 ,求数列
,求数列 的前
的前 项和
项和 .
. 的前
的前 项和为
项和为 ,
, ,
, 是
是 与
与 的等差中项(
的等差中项( ).
). 为等比数列;
为等比数列; ,使不等式
,使不等式 (
( 且
且
 中,已知
中,已知 .
. 是等差数列;
是等差数列; 满足
满足 ,求
,求 .
.