题目内容
9.半径为r的圆的面积S(r)πr2,周长C(r)=2πr,若将r看作(0,+∞)上的变量,则(πr2)′=2πr;对于半径为R的球,若将R看作(0,+∞)上的变量,请你写出类似于上述的式子:$(\frac{4}{3}π{R^3})'=4π{R^2}$.分析 圆的面积函数的导数等于圆的周长函数,类比得到球的体积函数的导数等于球的表面积函数,由二维空间推广到三维空间.
解答 解:V球=$\frac{4}{3}π{R}^{3}$,S球=4πR2,所以$(\frac{4}{3}π{R^3})'=4π{R^2}$.
故答案为:$(\frac{4}{3}π{R^3})'=4π{R^2}$.
点评 本题主要考查类比推理,类比推理一般步骤:①找出两类事物之间的相似性或者一致性.②用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(或猜想).

练习册系列答案
相关题目
14.把-1125°化成α+2kπ(0≤α<2π,k∈Z=)的形式是( )
| A. | -$\frac{π}{4}$-6π | B. | $\frac{7π}{4}$-6π | C. | -$\frac{π}{4}$-8π | D. | $\frac{7π}{4}$-8π |
1.函数$y=sin(2x+\frac{5π}{2})$的最小正周期是( )
| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | 4π |
18.已知三棱锥P-ABC的底面△ABC是正三角形,且PA=PB=PC,E、F是棱PA、BC的中点,记EF与平面PAB所成的角为α,EF与平面ABC所成的角为β,则α+β( )
| A. | 小于$\frac{π}{2}$ | B. | 等于$\frac{π}{2}$ | ||
| C. | 大于$\frac{π}{2}$ | D. | 与$\frac{π}{2}$的大小关系不能确定 |
19.已知命题p:x2+2x-3>0,命题q:x>a,若¬q的一个充分不必要条件是¬p,则实数a的取值范围是( )
| A. | a≥1 | B. | a>1 | C. | a≥-3 | D. | a>-3 |
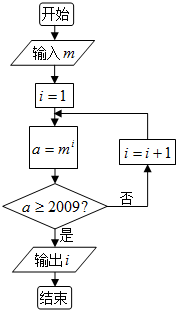 阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)
阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)