题目内容
已知不等式x2–3x+t<0的解集为{x|1<x<m, mÎR}
(1)求t, m的值;
(2)若f(x)= –x2+ax+4在(–∞,1)上递增,求不等式log a (–mx2+3x+2–t)<0的解集。
(1)求t, m的值;
(2)若f(x)= –x2+ax+4在(–∞,1)上递增,求不等式log a (–mx2+3x+2–t)<0的解集。
(1)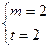 (2)
(2)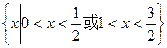
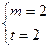 (2)
(2)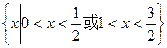
(1) 由条件得: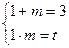 ,所以
,所以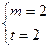 ,
,
(2)因为f(x)= –(x– )2+4+
)2+4+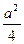 在(–∞,1)上递增,所以
在(–∞,1)上递增,所以 ≥1,a≥2 ,
≥1,a≥2 ,
log a (–mx2+3x+2–t)=" log" a (–2x2+3x)<0="log" a 1,所以 ,所以
,所以 ,所以
,所以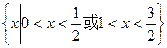 。
。
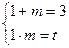 ,所以
,所以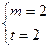 ,
,(2)因为f(x)= –(x–
 )2+4+
)2+4+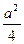 在(–∞,1)上递增,所以
在(–∞,1)上递增,所以 ≥1,a≥2 ,
≥1,a≥2 ,log a (–mx2+3x+2–t)=" log" a (–2x2+3x)<0="log" a 1,所以
 ,所以
,所以 ,所以
,所以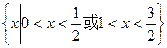 。
。
练习册系列答案
相关题目
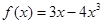 ,
,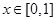 的最大值是( )
的最大值是( )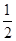
 ,
, 记
记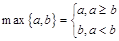 ,函数
,函数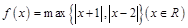 的最小值是 .
的最小值是 . 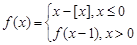 ,其中
,其中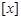 表示不超过
表示不超过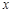 的最大整数,如
的最大整数,如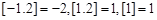 ,若
,若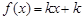 有三个不同的根,则实数
有三个不同的根,则实数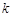 的取值范围是( )
的取值范围是( )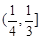
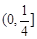
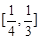
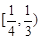
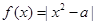 在区间[-1,1]上的最大值
在区间[-1,1]上的最大值 的最小值是 ( )
的最小值是 ( )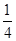

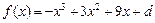 。
。 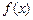 的单调区间;
的单调区间; 上的最小值为
上的最小值为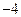 ,求实数
,求实数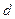 以及在该区间上的最大值.
以及在该区间上的最大值.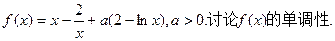

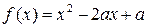 在区间
在区间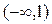 上有最小值,则函数
上有最小值,则函数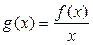 在区间
在区间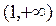 上一定( )
上一定( )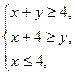 则目标函数
则目标函数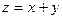 的最大值为
的最大值为  。
。