题目内容
已知函数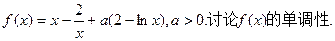

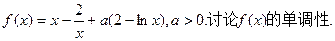

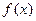 在
在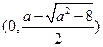 上单调递增,
上单调递增, 在
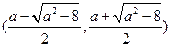 是上单调递减,
是上单调递减, 在
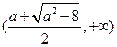 上单调递增.
上单调递增.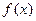 的定义域是(0,+
的定义域是(0,+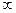 ),
),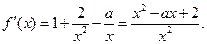
设
 ,二次方程
,二次方程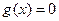 的判别式
的判别式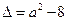 .
.① 当
 ,即
,即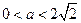 时,对一切
时,对一切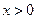 都有
都有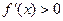 ,此时
,此时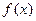 在
在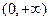 上是增函数。
上是增函数。② 当
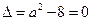 ,即
,即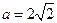 时,仅对
时,仅对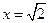 有
有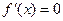 ,对其余的
,对其余的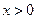 都有
都有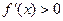 ,此时
,此时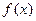 在
在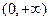 上也是增函数。
上也是增函数。③ 当
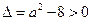 ,即
,即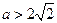 时,
时, 

方程
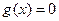 有两个不同的实根
有两个不同的实根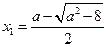 ,
,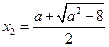 ,
,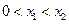 .
.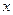 | 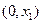 | 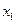 | 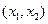 | 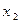 | 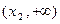 |
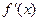 | + | 0 | _ | 0 | + |
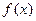 | 单调递增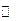 | 极大 | 单调递减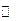 | 极小 | 单调递增 |
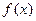 在
在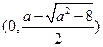 上单调递增, 在
上单调递增, 在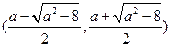 是上单调递减, 在
是上单调递减, 在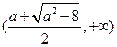 上单调递增.
上单调递增.
练习册系列答案
相关题目
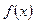 的定义域为R,且满足以下条件:1对任意的
的定义域为R,且满足以下条件:1对任意的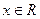 ,有
,有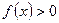 ;2对任意
;2对任意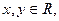 有
有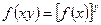 ;3
;3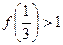
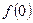 的值;
的值;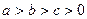 且a,b,c成等比数列,求证:
且a,b,c成等比数列,求证: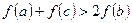 .
.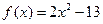 ,证明:(1)
,证明:(1)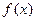 是偶函数; (2)
是偶函数; (2)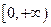 上是增加的
上是增加的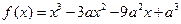 。
。 ,求函数
,求函数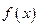 的极值;
的极值;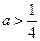 ,且当
,且当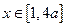 时,
时,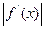
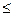 12a恒成立,试确定
12a恒成立,试确定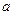 的取值范围。
的取值范围。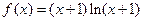 ,若对所有的
,若对所有的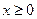 ,都有
,都有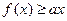 成立,求实数
成立,求实数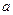 的取值范围.
的取值范围.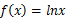 ,
,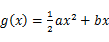 (
(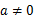 )
)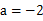 时,函数
时,函数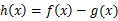 在其定义域是增函数,求b的取值范围。
在其定义域是增函数,求b的取值范围。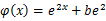 ,
,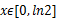 ,求函数
,求函数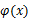 的最小值
的最小值 对称,且在区间
对称,且在区间 上是单调
上是单调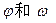 的值.
的值.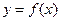 在
在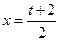 处取得最小值
处取得最小值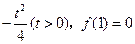 .
.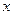 都满足等式
都满足等式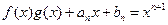 (
(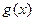 为多项式,
为多项式,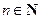 ),试用
),试用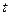 表示
表示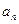 和
和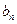 ;
;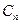 的方程为
的方程为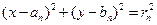 ,圆
,圆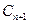 外切
外切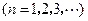 ,
,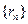 为各项都是正数的等比数列,记
为各项都是正数的等比数列,记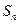 为前
为前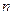 个圆的面积之和,
个圆的面积之和,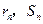 .
.