题目内容
10.设数列{an}的前n项和为Sn,已知${a_1}=1,{S_n}=n{a_n}-2n(n-1)(n∈{N^*})$.(1)求证:数列{an}为等差数列,并求出其通项公式;
(2)若${S_1}+\frac{S_2}{2}+\frac{S_3}{3}+…+\frac{S_m}{m}=400$,求正整数m的值.
分析 (1)运用数列的通项和前n项和的关系:n>1时,an=Sn-Sn-1,化简整理由等差数列的定义和通项公式,即可得到;
(2)运用等差数列的求和公式可得Sn=n(2n-1),再化简所给等式,由等差数列的求和公式,解方程可得m=20.
解答 解:(1)证明:当n≥2时,Sn=nan-2n(n-1),
∴Sn-1=(n-1)an-1-2(n-1)(n-2),
两式相减可得,an=nan-(n-1)an-1-4(n-1),
则(n-1)an=(n-1)an-1+4(n-1),
∴an=an-1+4,
∴{an}是首项为1,公差为4的等差数列,∴an=4n-3;
(2)Sn=$\frac{1}{2}$n(4n-2)=n(2n-1),
若${S_1}+\frac{S_2}{2}+\frac{S_3}{3}+…+\frac{S_m}{m}=400$,即为1+3+5+7+…+(2m-1)=400,
即有$\frac{1}{2}$m(1+2m-1)=400,即m2=400,
解得m=20.
点评 本题考查等差数列的定义、通项和求和公式的运用,注意运用数列的通项和前n项和的关系:当n=1时,a1=S1,n>1时,an=Sn-Sn-1,是解题的关键.

练习册系列答案
相关题目
1.如果a<b,那么下列不等式一定成立的是( )
| A. | c-a<c-b | B. | -2a>-2b | C. | a+c>b+c | D. | a+d>b+c |
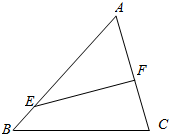 有一块三角形边角地,如图中△ABC,其中AB=8(百米),AC=6(百米),∠A=60°,某市为迎接2500年城庆,欲利用这块地修一个三角形形状的草坪(图中△AEF)供市民休闲,其中点E在边AB上,点F在边AC上,规划部门要求△AEF的面积占△ABC面积的一半,记△AEF的周长为l(百米).
有一块三角形边角地,如图中△ABC,其中AB=8(百米),AC=6(百米),∠A=60°,某市为迎接2500年城庆,欲利用这块地修一个三角形形状的草坪(图中△AEF)供市民休闲,其中点E在边AB上,点F在边AC上,规划部门要求△AEF的面积占△ABC面积的一半,记△AEF的周长为l(百米).