题目内容
(本题满分12分)设命题p:函数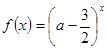 是R上的减函数,命题q:函数f(x)=x2-4x+3在
是R上的减函数,命题q:函数f(x)=x2-4x+3在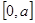 上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求
上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求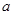 的取值范围.
的取值范围.
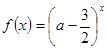 是R上的减函数,命题q:函数f(x)=x2-4x+3在
是R上的减函数,命题q:函数f(x)=x2-4x+3在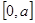 上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求
上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求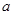 的取值范围.
的取值范围.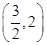 或
或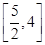 .
.由0<a-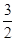 <1得
<1得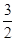 <a<
<a<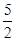 ,
,
∵f(x)=(x-2)2-1在[0,a]上的值域为[-1,3],则2≤a≤4,
∵p且q为假,p或q为真, ∴p、q为一真一假,
若p真q假,得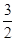 <a<2; 若p假q真,得
<a<2; 若p假q真,得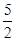 ≤a≤4.
≤a≤4.
综上可知,a的取值范围是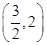 或
或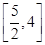 .
.
思路分析:p且q为假,p或q为真, ∴p、q为一真一假,分别求出两个命题真时对应的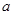 的范围,取交集即得a的取值范围是
的范围,取交集即得a的取值范围是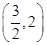 或
或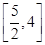 .
.
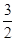 <1得
<1得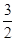 <a<
<a<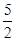 ,
,∵f(x)=(x-2)2-1在[0,a]上的值域为[-1,3],则2≤a≤4,
∵p且q为假,p或q为真, ∴p、q为一真一假,
若p真q假,得
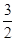 <a<2; 若p假q真,得
<a<2; 若p假q真,得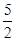 ≤a≤4.
≤a≤4.综上可知,a的取值范围是
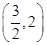 或
或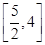 .
.思路分析:p且q为假,p或q为真, ∴p、q为一真一假,分别求出两个命题真时对应的
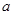 的范围,取交集即得a的取值范围是
的范围,取交集即得a的取值范围是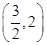 或
或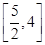 .
.
练习册系列答案
相关题目
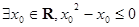 ”的否定是“
”的否定是“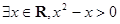 ”
” 为真”是命题“
为真”是命题“ 为真”的充分不必要条件
为真”的充分不必要条件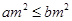 ,则
,则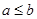 ”是假命题
”是假命题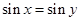 ,则
,则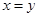 ”的逆否命题为真命题
”的逆否命题为真命题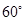 ”的逆命题;②“全等三角形的面积相等”的否命题;③“若
”的逆命题;②“全等三角形的面积相等”的否命题;③“若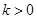 ,则方程
,则方程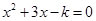 有实根”的逆否命题;④参数方程
有实根”的逆否命题;④参数方程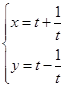 表示的曲线是双曲线.其中真命题的是________________.
表示的曲线是双曲线.其中真命题的是________________. 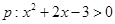 ;命题
;命题 ,若
,若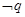 且
且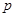 为真,求
为真,求 的取值范围.
的取值范围.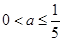 是
是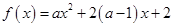 在区间
在区间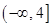 上为单调减函数的充要条件
上为单调减函数的充要条件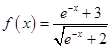 (e是自然对数的底数)的最小值为2.
(e是自然对数的底数)的最小值为2.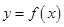 与它的反函数
与它的反函数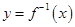 的图象若相交,则交点必在直线y="x" 上;
的图象若相交,则交点必在直线y="x" 上;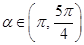 ,则
,则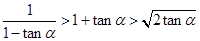 ;
;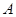 :若函数
:若函数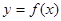 是幂函数,则函数
是幂函数,则函数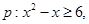 命题
命题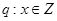 ;则使得当
;则使得当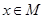 时,“
时,“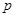 且
且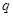 ”与“
”与“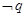 ” 同时为假命题的
” 同时为假命题的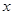 组成的集合
组成的集合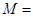 ;
;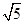 i,z2=
i,z2=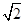 -
-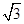 i,z3=-
i,z3=-