题目内容

19．已知函数f（x）=axlnx，x∈（0，+∞），其中a为实数，f′（x）为f（x）的导函数，若f′（1）=3，则a的值为3．

分析 根据导数的运算法则求导，再代入值计算即可．

解答 解：∵f′（x）=a（1+lnx），f′（1）=3，
∴a（1+ln1）=3，
解得a=3，
故答案为：3．

点评 本题考查了导数的运算法则，属于基础题．

练习册系列答案
相关题目
9．若tanx=$\sqrt{3}$，且角x∈（-π，π），则x=（　　）
A．-$\frac{2}{3}$π和$\frac{1}{3}$πB．-$\frac{1}{3}$π和$\frac{2}{3}$πC．-$\frac{5}{6}$π和$\frac{1}{6}$πD．-$\frac{1}{6}$π和$\frac{5}{6}$π
10．在平行四边形ABCD中，$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}$=$\overrightarrow{AC}$，$\frac{\overrightarrow{AB}•\overrightarrow{AD}}{|\overrightarrow{AB}||\overrightarrow{AD}|}$=$\frac{1}{2}$，E为CD的中点，若$\overrightarrow{AC}$•$\overrightarrow{BE}$=3，则|$\overrightarrow{AB}$|=2$\sqrt{3}$．
7．求d的最大、最小值．
d=$\frac{|2cosθ+\sqrt{3}sinθ-8|}{\sqrt{2}}$．
14．当x∈[$\frac{π}{6}$，$\frac{7π}{6}$]时，函数y=3-sinx-2cos2x的最大值是2．
4．计算：[（lg$\frac{1}{2}$）-lg50]÷100${\;}^{\frac{1}{2}}$．
11．设非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$，$\overrightarrow{d}$满足$\overrightarrow{d}$=（$\overrightarrow{a}$•$\overrightarrow{b}$）$\overrightarrow{c}$-（$\overrightarrow{a}$•$\overrightarrow{c}$）$\overrightarrow{b}$，则$\overrightarrow{a}$与$\overrightarrow{d}$（　　）
A．相等B．共线C．方向相同D．垂直
8．解不等式30x2+ax＜a2．
9．阅读如图所示的程序框图，若输出的S等于210-1，则输出的k的值可以是（　　）
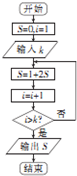
A．9B．10C．11D．12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网