题目内容
在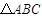 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为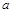 、
、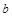 、
、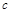 ,已知向量
,已知向量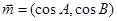 、
、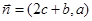 ,且
,且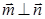 .
.
(1)求角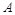 的大小;
的大小;
(2)若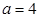 ,求
,求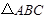 面积的最大值.
面积的最大值.
(1)  (2)
(2)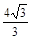
解析试题分析:
(1)根据条件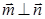 ,利用
,利用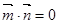 可得一个边角关系式,因为要求角,所以利用正弦定理的性质
可得一个边角关系式,因为要求角,所以利用正弦定理的性质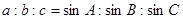 将边化为角,化简关系式,可得所求角,
将边化为角,化简关系式,可得所求角,
(2)根据(1)的结论,选择面积公式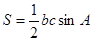 ,所以得求出
,所以得求出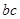 范围,根据余弦定理
范围,根据余弦定理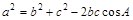 ,利用不等式性质可得到
,利用不等式性质可得到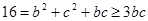 ,从而求出面积的最值.
,从而求出面积的最值.
(1)∵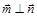 ∴
∴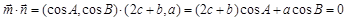
由正弦定理可得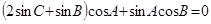 ,即
,即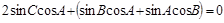 ,
,
整理可得 .
.
∵0<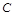 <
<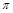 ,
,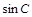 >0, ∴
>0, ∴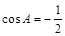 ∴
∴  .
.
(2)由余弦定理,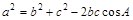 ,即
,即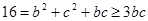 ,故
,故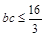 .
.
故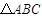 的面积为
的面积为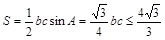
当且仅当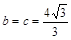 时,
时, 面积取得最大值
面积取得最大值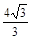 .
.
考点:向量垂直关系;正弦定理;余弦定理;不等式性质;三角形面积公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是
是 的三个内角,其对边分别为
的三个内角,其对边分别为 且
且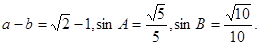
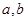 的值; (2)若角A为锐角,求角
的值; (2)若角A为锐角,求角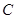 和边
和边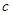 的值.
的值. 中,
中,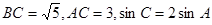
 的值;
的值; ,函数
,函数 的最小正周期为
的最小正周期为 .
. 的值;
的值; 的三边
的三边 、
、 、
、 满足:
满足: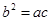 ,且边
,且边 ,若关于
,若关于 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.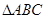 中,角
中,角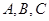 所对的边分别为
所对的边分别为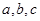 ,点
,点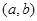 在直线
在直线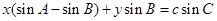 上.
上. 的值;
的值;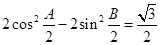 ,且
,且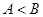 ,求
,求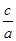 .
.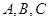 的对边分别为
的对边分别为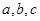 ,且
,且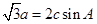 .
.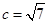 ,且△ABC的面积为
,且△ABC的面积为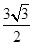 ,求
,求 的值。
的值。 ,求C
,求C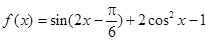 .
. 的单调增区间;
的单调增区间;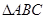 中,
中, 分别是角
分别是角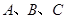 的对边,且
的对边,且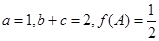 ,求
,求