题目内容
已知函数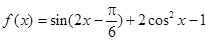 .
.
(1)求函数 的单调增区间;
的单调增区间;
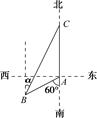
(2)在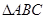 中,
中, 分别是角
分别是角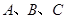 的对边,且
的对边,且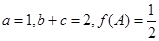 ,求
,求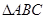 的面积.
的面积.
(1) (2)
(2)
解析试题分析:(1)研究三角函数性质,现将三角函数化为基本三角函数,即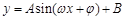 型. 先利用倍角公式及两角和与差正弦化简
型. 先利用倍角公式及两角和与差正弦化简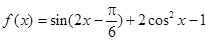 为
为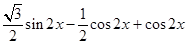 =
=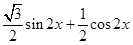 ,再利用配角公式化为
,再利用配角公式化为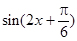 ,最后结合基本三角函数图像求出函数
,最后结合基本三角函数图像求出函数 的单调递增区间为
的单调递增区间为 .(2)解三角形问题,一般利用正余弦定理进行边角转化,先根据
.(2)解三角形问题,一般利用正余弦定理进行边角转化,先根据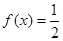 ,求出角A,再根据一角三边关系,利用余弦定理求
,求出角A,再根据一角三边关系,利用余弦定理求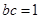 ,最后代入面积公式
,最后代入面积公式
试题解析:(1)∵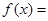
 =
=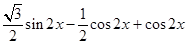
=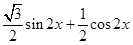 =
=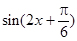 . 3分
. 3分
∴函数 的单调递增区间是
的单调递增区间是 . 5分
. 5分
(2)∵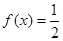 ,∴
,∴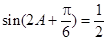 .
.
又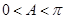 ,∴
,∴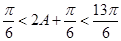 .
.
∴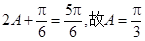 . 7分
. 7分
在 中,∵
中,∵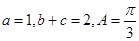 ,
,
∴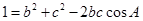 ,即
,即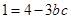 .
.
∴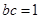 . 10分
. 10分
∴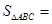
 12分
12分
考点:三角函数化简,余弦定理

练习册系列答案
相关题目
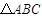 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为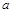 、
、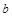 、
、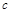 ,已知向量
,已知向量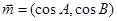 、
、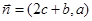 ,且
,且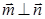 .
.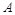 的大小;
的大小;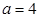 ,求
,求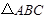 面积的最大值.
面积的最大值. cos4x (1)求f(x)的最小正周期及最大值。
cos4x (1)求f(x)的最小正周期及最大值。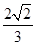 ,f(
,f(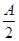 )=-
)=-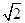 ,b=
,b=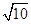 ,求c;
,求c;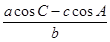 的取值范围.
的取值范围. 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、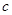 .已知
.已知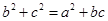 .
.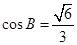 ,
,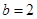 ,求
,求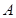 、
、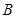 、
、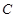 为
为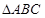 的三内角,且其对边分别为
的三内角,且其对边分别为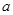 、
、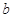 、
、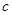 ,若
,若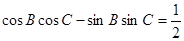 .
.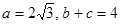 ,求
,求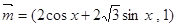 ,
, ,且
,且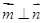 .
.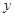 表示为
表示为 的函数
的函数 ,并求
,并求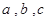 分别为
分别为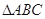 的三个内角
的三个内角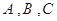 对应的边长,若
对应的边长,若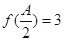 ,且
,且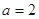 ,
,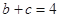 ,求
,求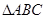 中,内角
中,内角 、
、 、
、 的对边分别为
的对边分别为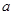 、
、 、
、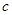 ,且
,且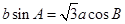 .
.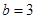 ,
, ,求
,求