题目内容
在锐角△ABC中,角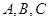 的对边分别为
的对边分别为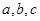 ,且
,且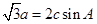 .
.
(1)确定角C的大小;
(2)若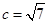 ,且△ABC的面积为
,且△ABC的面积为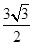 ,求
,求 的值。
的值。
(1)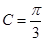 ;(2)
;(2)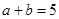 .
.
解析试题分析:(1)通过正弦定理把题设等式中的边转化成角的正弦,化简整理求得sinC的值,进而求得C.(2)先利用面积公式求得ab的值,进而利用余弦定理求得a2+b2-ab,最后联立变形求得a+b的值.
(1)∵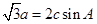 ,由正弦定理得
,由正弦定理得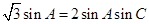 , 2分
, 2分
∵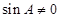 ∴
∴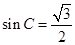 ,又△ABC为锐角三角形
,又△ABC为锐角三角形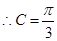 6分
6分
(2)解1:∵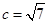 ,且△ABC的面积为
,且△ABC的面积为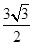 ,
,
又由(1)知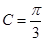 ,由面积公式得
,由面积公式得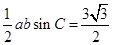 ,
,
即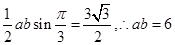 8分
8分
又由余弦定理得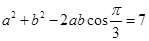 , 即
, 即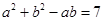
∴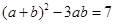 , 即
, 即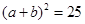 ∴
∴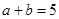 12分 .
12分 .
考点:1.余弦定理的应用;2.正弦定理.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 ,
, ,
, .
.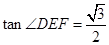 时,求
时,求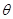 的大小;
的大小;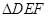 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时
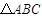 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为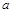 、
、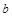 、
、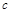 ,已知向量
,已知向量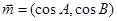 、
、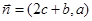 ,且
,且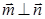 .
.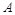 的大小;
的大小;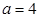 ,求
,求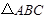 面积的最大值.
面积的最大值.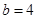 ,
,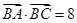 .
.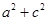 的值;
的值;  的值域.
的值域. 上的两点,点C是圆
上的两点,点C是圆 轴的正半轴的交点,将锐角
轴的正半轴的交点,将锐角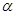 的终边
的终边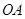 按逆时针方向旋转
按逆时针方向旋转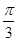 到
到 .
.
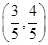 ,求
,求 的值;
的值; ,并求
,并求
 cos4x (1)求f(x)的最小正周期及最大值。
cos4x (1)求f(x)的最小正周期及最大值。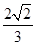 ,f(
,f(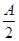 )=-
)=-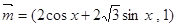 ,
, ,且
,且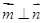 .
.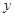 表示为
表示为 的函数
的函数 ,并求
,并求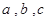 分别为
分别为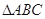 的三个内角
的三个内角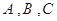 对应的边长,若
对应的边长,若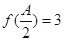 ,且
,且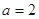 ,
,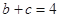 ,求
,求