题目内容
【题目】设函数f(x)=|x﹣2|+|x+a|(a∈R).
(1)若a=1时,求不等式f(x)≥4的解集;
(2)若不等式f(x)≤2x的解集为[1,+∞),求a的值.
【答案】
(1)解:a=1时,f(x)≥4可化为|x﹣2|+|x+1|≥4.
x<﹣1时,2﹣x﹣x﹣1≥4,∴x≤﹣ ![]() ;
;
﹣1≤x≤2时,2﹣x+x+1≥4,无解;
x>2时,x﹣2+x+1≥4,∴x≥ ![]() .
.
综上所述,不等式的解集为{x|x≤﹣ ![]() 或x≥
或x≥ ![]() }
}
(2)解:∵不等式f(x)≤2x的解集为[1,+∞),
∴|x﹣2|+|x+a|=2x的一个根是1,
∴a=0或﹣2.
a=0时,由|x﹣2|+|x|≤2x,解得x≥1,合题意;
a=﹣2时,由2|x﹣2|≤2x,解得x≥1,合题意;
综上所述,a=0或﹣2
【解析】(1)a=1时,f(x)≥4可化为|x﹣2|+|x+1|≥4.去掉绝对值符号解不等式,即可求不等式f(x)≥4的解集;(2)若不等式f(x)≤2x的解集为[1,+∞),则|x﹣2|+|x+a|=2x的一个根是1,求出a,再进行验证,即可求a的值.
【考点精析】通过灵活运用绝对值不等式的解法,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号即可以解答此题.

【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响,部分统计数据如右表,则下列说法正确的是( )
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
参考公式: 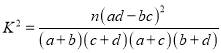 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A. 有99.9%的把握认为使用智能手机对学习有影响.
B. 有99.9%的把握认为使用智能手机对学习无影响.
C. 在犯错误的概率不超过0.005的前提下认为使用智能手机对学习有影响.
D. 在犯错误的概率不超过0.005的前提下认为使用智能手机对学习无影响.

