题目内容
【题目】设函数f(x)=![]() ax2-1-lnx,其中a∈R.
ax2-1-lnx,其中a∈R.
(1)若a=0,求过点(0,-1)且与曲线y=f(x)相切的直线方程;
(2)若函数f(x)有两个零点x1,x2,
① 求a的取值范围;
② 求证:f ′(x1)+f ′(x2)<0.
【答案】(1) y=-![]() x-1 (2) ① (0,e).②见解析
x-1 (2) ① (0,e).②见解析
【解析】试题分析:(1)设切点为T(x0,-1-lnx0),得切线:y+1+lnx0=-![]() ( x-x0),将点(0,-1)代入求解即可;
( x-x0),将点(0,-1)代入求解即可;
(2)①求导f ′(x)=![]() ,讨论a≤0,和a>0时函数的单调性求解即可;
,讨论a≤0,和a>0时函数的单调性求解即可;
②由x1,x2是函数f(x)的两个零点(不妨设x1<x2),得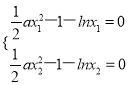 ,两式作差得a(x1+x2)=
,两式作差得a(x1+x2)=![]() ,代入要证得式子得2ln
,代入要证得式子得2ln![]() +
+![]() -
-![]() >0,令h(x)=2lnx+
>0,令h(x)=2lnx+![]() -x,x∈(0,1),求导利用单调性求最值即可证得.
-x,x∈(0,1),求导利用单调性求最值即可证得.
试题解析:
(1)当a=0时,f(x)=-1-lnx,f ′(x)=-![]() .
.
设切点为T(x0,-1-lnx0),
则切线方程为:y+1+lnx0=-![]() ( x-x0).
( x-x0).
因为切线过点(0,-1),所以 -1+1+ln x0=-![]() (0-x0),解得x0=e.
(0-x0),解得x0=e.
所以所求切线方程为y=-![]() x-1.
x-1.
(2)① f ′(x)=ax-![]() =
=![]() ,x>0.
,x>0.
(i) 若a≤0,则f ′(x)<0,所以函数f(x)在(0,+∞)上单调递减,
从而函数f(x)在(0,+∞)上至多有1个零点,不合题意.
(ii)若a>0,由f ′(x)=0,解得x=![]() .
.
当0<x<![]() 时, f ′(x)<0,函数f(x)单调递减;当x>时, f ′(x)>0,f(x)单调递增,
时, f ′(x)<0,函数f(x)单调递减;当x>时, f ′(x)>0,f(x)单调递增,
所以f(x)min=f(![]() )=
)=![]() -ln
-ln![]() -1=-
-1=-![]() -ln
-ln![]() .
.
要使函数f(x)有两个零点,首先 -![]() -ln
-ln![]() <0,解得0<a<e.
<0,解得0<a<e.
当0<a<e时,![]() >
>![]() >
>![]() .
.
因为f(![]() )=
)=![]() >0,故f(
>0,故f(![]() )·f(
)·f(![]() )<0.
)<0.
又函数f(x)在(0,![]() )上单调递减,且其图像在(0,
)上单调递减,且其图像在(0,![]() )上不间断,
)上不间断,
所以函数f(x)在区间(0,![]() )内恰有1个零点.
)内恰有1个零点.
考察函数g(x)=x-1-lnx,则g′(x)=1-![]() =
=![]() .
.
当x∈(0,1)时,g′(x)<0,函数g(x)在(0,1)上单调递减;
当x∈(1,+∞)时,g′(x)>0,函数g(x)在(1,+∞)上单调递增,
所以g(x)≥g(1)=0,故f(![]() )=
)=![]() -1-ln
-1-ln![]() ≥0.
≥0.
因为![]() -
-![]() =
=![]() >0,故
>0,故![]() >
>![]() .
.
因为f(![]() )·f(
)·f(![]() )≤0,且f(x)在(
)≤0,且f(x)在(![]() ,+∞)上单调递增,其图像在(
,+∞)上单调递增,其图像在(![]() ,+∞)上不间断,
,+∞)上不间断,
所以函数f(x)在区间(![]() ,
,![]() ] 上恰有1个零点,即在(
] 上恰有1个零点,即在(![]() ,+∞)上恰有1个零点.
,+∞)上恰有1个零点.
综上所述,a的取值范围是(0,e).
②由x1,x2是函数f(x)的两个零点(不妨设x1<x2),得 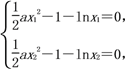
两式相减,得 ![]() a(x12-x22)-ln
a(x12-x22)-ln![]() =0,即
=0,即![]() a(x1+x2) (x1-x2)-ln
a(x1+x2) (x1-x2)-ln![]() =0,
=0,
所以a(x1+x2)=![]() .
.
f ′(x1)+f ′(x2)<0等价于ax1-![]() +ax2-
+ax2-![]() <0,即a(x1+x2)-
<0,即a(x1+x2)-![]() -
-![]() <0,
<0,
即![]() -
-![]() -
-![]() <0,即2ln
<0,即2ln![]() +
+![]() -
-![]() >0.
>0.
设h(x)=2lnx+![]() -x,x∈(0,1).则h′(x)=
-x,x∈(0,1).则h′(x)=![]() -
-![]() -1=
-1=![]() =-
=-![]() <0,
<0,
所以函数h(x)在(0,1)单调递减,所以h(x)>h(1)=0.
因为![]() ∈(0,1),所以2ln
∈(0,1),所以2ln![]() +
+![]() -
-![]() >0,
>0,
即f ′(x1)+f ′(x2)<0成立.

 精英口算卡系列答案
精英口算卡系列答案【题目】某小型企业甲产品生产的投入成本![]() (单位:万元)与产品销售收入
(单位:万元)与产品销售收入![]() (单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
(单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大(![]() )?
)?
相关公式: 
 ,
, ![]() .
.
【答案】(1)![]() .(2)投入成本20万元的毛利率更大.
.(2)投入成本20万元的毛利率更大.
【解析】试题分析:(1)由回归公式,解得线性回归方程为![]() ;(2)当
;(2)当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,当
,当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,故投入成本20万元的毛利率更大。
,故投入成本20万元的毛利率更大。
试题解析:
(1)![]() ,
, ![]() ,
,

![]() ,
, ![]() ,故
,故![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(2)当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,
,
当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,
,
故投入成本20万元的毛利率更大.
【题型】解答题
【结束】
21
【题目】如图,在正方体![]() 中,
中, ![]() 分别是棱
分别是棱![]() 的中点,
的中点, ![]() 为棱
为棱![]() 上一点,且异面直线
上一点,且异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.

(1)证明: ![]() 为
为![]() 的中点;
的中点;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.


