题目内容
【题目】设函数f(x)的定义域为R,并且图象关于y轴对称,当x≤-1时,y=f(x)的图象是经过点(-2,0)与(-1,1)的射线,又在y=f(x)的图象中有一部分是顶点在(0,2),且经过点(1,1)的一段抛物线.
(1)试求出函数f(x)的表达式,作出其图象;
(2)根据图象说出函数的单调区间,以及在每一个单调区间上函数是增函数还是减函数.
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用待定系数法求出![]() ,结合奇偶性求出
,结合奇偶性求出![]() ,最后利用待定系数法求出
,最后利用待定系数法求出![]() ,作出图即可;(2)根据图形的上升、下降趋势得到单调性.
,作出图即可;(2)根据图形的上升、下降趋势得到单调性.
(1)当x≤-1时,设f(x)=ax+b(a≠0),由已知得![]()
解得![]() ,所以f(x)=x+2(x≤-1).
,所以f(x)=x+2(x≤-1).
由于函数图象关于y轴对称,则由x≥1,得-x≤-1,f(-x)=-x+2,
且f(-x)=f(x),所以f(x)=-x+2(x≥1).
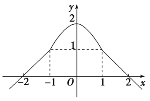
当-1<x<1时,设f(x)=mx2+2,由已知得m=-1,即f(x)=-x2+2(-1<x<1),所以函数f(x)的表达式为f(x)=图象如图所示:
 .
.
(2)从图象可看出,函数f(x)的单调区间有(-∞,-1],(-1,0],(0,1),[1,+∞).
其中,f(x)在区间(-∞,-1]和(-1,0]上是增函数;在区间(0,1)和[1,+∞)上是减函数.

【题目】某小型企业甲产品生产的投入成本![]() (单位:万元)与产品销售收入
(单位:万元)与产品销售收入![]() (单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
(单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大(![]() )?
)?
相关公式: 
 ,
, ![]() .
.
【答案】(1)![]() .(2)投入成本20万元的毛利率更大.
.(2)投入成本20万元的毛利率更大.
【解析】试题分析:(1)由回归公式,解得线性回归方程为![]() ;(2)当
;(2)当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,当
,当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,故投入成本20万元的毛利率更大。
,故投入成本20万元的毛利率更大。
试题解析:
(1)![]() ,
, ![]() ,
,

![]() ,
, ![]() ,故
,故![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(2)当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,
,
当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,
,
故投入成本20万元的毛利率更大.
【题型】解答题
【结束】
21
【题目】如图,在正方体![]() 中,
中, ![]() 分别是棱
分别是棱![]() 的中点,
的中点, ![]() 为棱
为棱![]() 上一点,且异面直线
上一点,且异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.

(1)证明: ![]() 为
为![]() 的中点;
的中点;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【题目】某中学对男女学生是否喜爱古典音乐进行了一个调查,调查者对学校高三年级随机抽取了100名学生,调查结果如表:
喜爱 | 不喜爱 | 总计 | |
男学生 | 60 | 80 | |
女学生 | |||
总计 | 70 | 30 |
附:K2= ![]()
P(K2≥k0) | 0.100 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
(1)完成如表,并根据表中数据,判断是否有95%的把握认为“男学生和女学生喜欢古典音乐的程度有差异”;
(2)从以上被调查的学生中以性别为依据采用分层抽样的方式抽取10名学生,再从这10名学生中随机抽取5名学生去某古典音乐会的现场观看演出,求正好有X个男生去观看演出的分布列及期望.