Question

11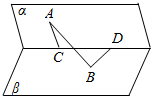．如图，二面角α-l-β为60°，点A、B分别为平面α和平面β上的点，点A到l的距离为|AC|=4，点B到l的距离为|BD|=5，|CD|=6，求：
（1）A与B两点间的距离|AB|；
（2）异面直线AB、CD所成角的正切值．

Answer 1

分析 （1）由$\overrightarrow{AB}$=$\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DB}$，能求出|AB|的值．
（2）在平面α内作DE∥AC，过A作AE∥CD，交DE于点E，连结BE，由已知得ACDE是矩形，且AC=4，AE=6，从而∠BAE是异面直线AB、CD所成角（或所成角的补角），由此利用余弦定理能求出异面直线AB、CD所成角的正切值．

解答 解：（1）∵二面角α-l-β为60°，点A、B分别为平面α和平面β上的点，
点A到l的距离为|AC|=4，点B到l的距离为|BD|=5，|CD|=6，
∴$\overrightarrow{AB}$=$\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DB}$，
∴${\overrightarrow{AB}}^{2}$=（$\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DB}$）²
=${\overrightarrow{AC}}^{2}+{\overrightarrow{CD}}^{2}+{\overrightarrow{DB}}^{2}$+2$\overrightarrow{AC}•\overrightarrow{DB}$
=16+36+25+2×4×5×cos120°
=57，
∴|AB|=$\sqrt{57}$．
（2）在平面α内作DE∥AC，过A作AE∥CD，交DE于点E，连结BE，
由已知得ACDE是矩形，且AC=4，AE=6，
∵CD∥AE，∴∠BAE是异面直线AB、CD所成角（或所成角的补角），
在△BDE中，BD=5，DE=AC=4，∠BDE=60°，
∴BE=$\sqrt{B{D}^{2}+D{E}^{2}-2×BD×DE×cos60°}$=$\sqrt{25+16-2×5×4×\frac{1}{2}}$=$\sqrt{21}$，
∴cos∠BAE=$\frac{A{E}^{2}+A{B}^{2}-B{E}^{2}}{2×AE×AB}$=$\frac{36+57-21}{2×6×\sqrt{57}}$=$\frac{6\sqrt{57}}{57}$，
∴tan∠BAE=$\frac{\sqrt{21}}{6}$，
∴异面直线AB、CD所成角的正切值为$\frac{\sqrt{21}}{6}$．

点评 本题考查空间两点间距离的求法，考查异面直线所成角的正切值的求法，是中档题，解题时要认真审题，注意空间思维能力和余弦定理的合理运用．