题目内容
1.圆柱的轴截面为边长为a的正方形,则此圆柱的全面积为$\frac{3π}{2}a$.分析 根据已知求出底面半径和高,然后求出表面积.
解答 解:∵圆柱的轴截面为边长为a的正方形,
∴圆柱底面半径r=$\frac{1}{2}$$\sqrt{a}$,
圆柱的高h=$\sqrt{a}$,
故圆锥的全面积:S=2πr(r+h)=$\frac{3π}{2}a$,
故答案为:$\frac{3π}{2}a$.
点评 本题是基础题,考查圆柱的表面积与轴截面的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.观察下列等式:13=1,23=3+5,33=7+9+11,43=13+15+17+19,…若某数n3按上述规律展开后,发现等式右边含有“2015”这个数,则n=( )
| A. | 44 | B. | 45 | C. | 46 | D. | 47 |
16.变量 x、y满足线性约束条件$\left\{\begin{array}{l}{3x+y-2≤0}\\{y-x≤2}\\{y≥x-1}\end{array}\right.$,则目标函数z=(k+1)x-y,仅在点(0,2)取得最小值,则k的取值范围是( )
| A. | k<-4 | B. | -4<k<0> | C. | -2<k<0 | D. | k>0 |
13.已知p:2+2=5,q:3≥2,则下列判断中,错误的是( )
| A. | p或q为真,非q为假 | B. | p或q为真,非p为真 | ||
| C. | p且q为假,非p为假 | D. | p且q为假,p或q为真 |
10.已知tanα+sinα=a(a≠0),tanα-sinα=b,则cosα等于( )
| A. | $\frac{a+b}{2}$ | B. | $\frac{a-b}{2}$ | C. | $\frac{a+b}{a-b}$ | D. | $\frac{a-b}{a+b}$ |
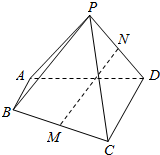 如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.
如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.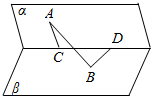 如图,二面角α-l-β为60°,点A、B分别为平面α和平面β上的点,点A到l的距离为|AC|=4,点B到l的距离为|BD|=5,|CD|=6,求:
如图,二面角α-l-β为60°,点A、B分别为平面α和平面β上的点,点A到l的距离为|AC|=4,点B到l的距离为|BD|=5,|CD|=6,求: