题目内容
2.已知双曲线$\frac{{x}^{2}}{m}$-y2=1(m>0)的离心率为$\frac{2\sqrt{3}}{3}$,则m的值为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | 3 | C. | 8 | D. | $\frac{\sqrt{3}}{2}$ |
分析 通过双曲线的几何量,结合离心率直接求解即可.
解答 解:双曲线$\frac{{x}^{2}}{m}$-y2=1(m>0),
可得a=$\sqrt{m}$,b=1,c=$\sqrt{m+1}$,
双曲线$\frac{{x}^{2}}{m}$-y2=1(m>0)的离心率为$\frac{2\sqrt{3}}{3}$,
可得:$\frac{\sqrt{m+1}}{\sqrt{m}}$=$\frac{2\sqrt{3}}{3}$,
解得m=3.
故选:B.
点评 本题考查双曲线的解得性质的应用,考查计算能力.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
13.已知p:2+2=5,q:3≥2,则下列判断中,错误的是( )
| A. | p或q为真,非q为假 | B. | p或q为真,非p为真 | ||
| C. | p且q为假,非p为假 | D. | p且q为假,p或q为真 |
10.已知tanα+sinα=a(a≠0),tanα-sinα=b,则cosα等于( )
| A. | $\frac{a+b}{2}$ | B. | $\frac{a-b}{2}$ | C. | $\frac{a+b}{a-b}$ | D. | $\frac{a-b}{a+b}$ |
7.直线y=-$\sqrt{3}$(x-2)截圆x2+y2=4所得的劣弧所对的圆心角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{3}$ |
12.在如图的表格中,每格填上一个数字后,使每一行成等差数列,每一列成等比数列,则a+b的值为( )
| 1 | 2 | ||
| 0.5 | 1 | ||
| a | b |
| A. | 1 | B. | $\frac{17}{16}$ | C. | $\frac{19}{16}$ | D. | $\frac{9}{8}$ |
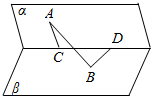 如图,二面角α-l-β为60°,点A、B分别为平面α和平面β上的点,点A到l的距离为|AC|=4,点B到l的距离为|BD|=5,|CD|=6,求:
如图,二面角α-l-β为60°,点A、B分别为平面α和平面β上的点,点A到l的距离为|AC|=4,点B到l的距离为|BD|=5,|CD|=6,求: