题目内容
(本题满分12分)
已知函数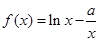 ;
;
(1)当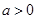 时,判断
时,判断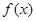 在定义域上的单调性;
在定义域上的单调性;
(2)求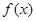 在
在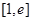 上的最小值.
上的最小值.
已知函数
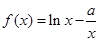 ;
;(1)当
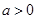 时,判断
时,判断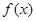 在定义域上的单调性;
在定义域上的单调性;(2)求
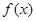 在
在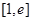 上的最小值.
上的最小值.(1)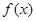 在
在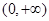 上是单调递增函数.
上是单调递增函数.
(2) 当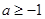 时 ,
时 ,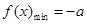 ;
;
当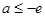 时,
时, 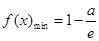 ;
;
当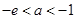 时 ,
时 , 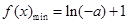 -
-
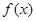 在
在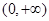 上是单调递增函数.
上是单调递增函数.(2) 当
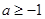 时 ,
时 ,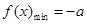 ;
;当
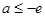 时,
时, 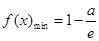 ;
;当
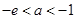 时 ,
时 , 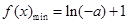 -
-试题分析:解:(Ⅰ)由题意:
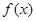 的定义域为
的定义域为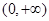 ,且
,且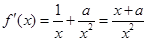 .
.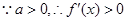 ,故
,故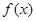 在
在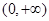 上是单调递增函数. ---------------4分
上是单调递增函数. ---------------4分 (Ⅱ)由(1)可知:
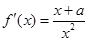
① 若
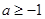 ,则
,则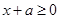 ,即
,即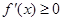 在
在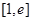 上恒成立,此时
上恒成立,此时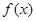 在
在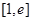 上为增函数,
上为增函数,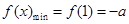 ------------------6分
------------------6分② 若
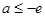 ,则
,则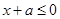 ,即
,即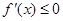 在
在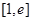 上恒成立,此时
上恒成立,此时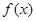 在
在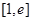 上为减函数,
上为减函数,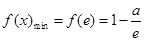 ------------------8分
------------------8分③ 若
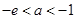 ,令
,令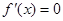 得
得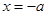 ,
,当
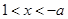 时,
时,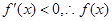 在
在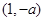 上为减函数,
上为减函数,当
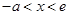 时,
时,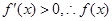 在
在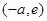 上为增函数,
上为增函数,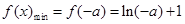 ------------------11分
------------------11分综上可知:当
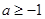 时 ,
时 ,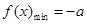 ;
;当
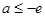 时,
时, 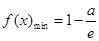 ;
;当
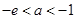 时 ,
时 , 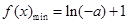 -----------------12分
-----------------12分点评:根据导数的符号判定函数的单调性是解题的关键,属于基础题。

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 的图象是连续不断的曲线,且有如下的对应值表
的图象是连续不断的曲线,且有如下的对应值表

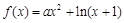 .
.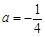 时,求函数
时,求函数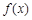 的单调区间;
的单调区间;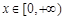 时,函数
时,函数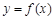 图象上的点都在
图象上的点都在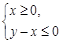 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.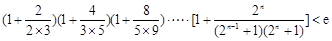 (其中
(其中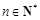 ,e是自然对数的底数).
,e是自然对数的底数). 的导函数的部分图象为( )
的导函数的部分图象为( )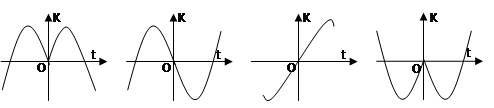
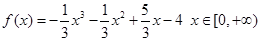 .
. 的极值;
的极值; 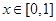 时,求
时,求 ,函数
,函数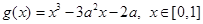 ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.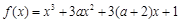 有极大值和极小值,则
有极大值和极小值,则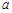 的取值范围是__ .
的取值范围是__ .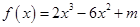 (
(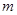 为常数)在
为常数)在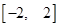 上有最大值3,那么此函数在
上有最大值3,那么此函数在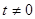 ,点P(
,点P(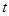 ,0)是函数
,0)是函数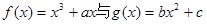 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.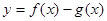 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求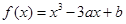 在点
在点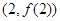 处与直线
处与直线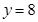 相切,则
相切,则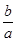 为 .
为 .