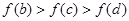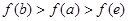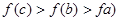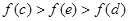题目内容
(本小题满分14分) 已知函数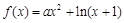 .
.
(Ⅰ)当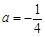 时,求函数
时,求函数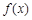 的单调区间;
的单调区间;
(Ⅱ)当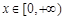 时,函数
时,函数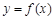 图象上的点都在
图象上的点都在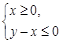 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.
(Ⅲ)求证: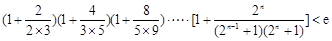 (其中
(其中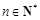 ,e是自然对数的底数).
,e是自然对数的底数).
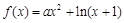 .
.(Ⅰ)当
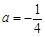 时,求函数
时,求函数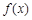 的单调区间;
的单调区间;(Ⅱ)当
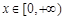 时,函数
时,函数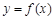 图象上的点都在
图象上的点都在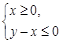 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.(Ⅲ)求证:
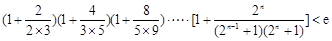 (其中
(其中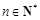 ,e是自然对数的底数).
,e是自然对数的底数).(Ⅰ)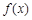 的单调递增区间为
的单调递增区间为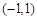 ,单调递减区间为
,单调递减区间为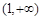 .
.
(Ⅱ)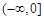 .(Ⅲ)见解析。
.(Ⅲ)见解析。
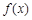 的单调递增区间为
的单调递增区间为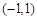 ,单调递减区间为
,单调递减区间为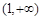 .
.(Ⅱ)
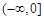 .(Ⅲ)见解析。
.(Ⅲ)见解析。本试题主要是考出了导数在研究函数中的运用。
(1)因为当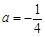 时,
时,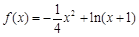 (
( ),
),
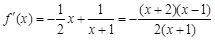 (
( ),
),
由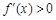 解得
解得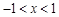 ,由
,由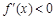 解得
解得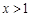 .得到单调区间。
.得到单调区间。
(2)因函数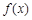 图象上的点都在
图象上的点都在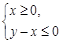 所表示的平面区域内,则当
所表示的平面区域内,则当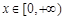 时,不等式
时,不等式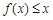 恒成立,即
恒成立,即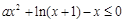 恒成立,设
恒成立,设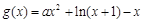 (
(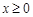 ),只需
),只需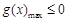 即可,转化思想的运用。
即可,转化思想的运用。
(3)据(Ⅱ)知当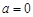 时,
时,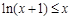 在
在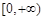 上恒成立(或另证
上恒成立(或另证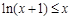 在区间
在区间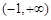 上恒成立)结合放缩法得到结论。
上恒成立)结合放缩法得到结论。
(Ⅰ)当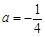 时,
时,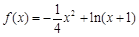 (
( ),
),
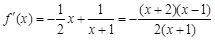 (
( ),
),
由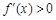 解得
解得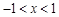 ,由
,由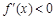 解得
解得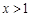 .
.
故函数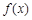 的单调递增区间为
的单调递增区间为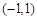 ,单调递减区间为
,单调递减区间为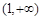 .········· 4分
.········· 4分
(Ⅱ)因函数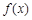 图象上的点都在
图象上的点都在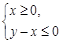 所表示的平面区域内,则当
所表示的平面区域内,则当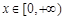 时,不等式
时,不等式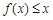 恒成立,即
恒成立,即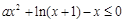 恒成立,设
恒成立,设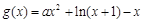 (
(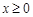 ),只需
),只需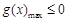 即可. 5分
即可. 5分
由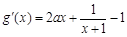
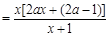 ,
,
(ⅰ)当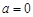 时,
时, 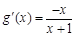 ,当
,当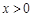 时,
时,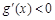 ,函数
,函数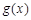 在
在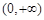 上单调递减,故
上单调递减,故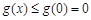 成立. 6分
成立. 6分
(ⅱ)当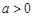 时,由
时,由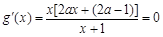 ,因
,因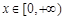 ,所以
,所以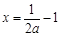 ,
,
①若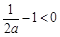 ,即
,即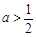 时,在区间
时,在区间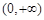 上,
上,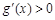 ,则函数
,则函数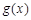 在
在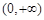 上单调递增,
上单调递增,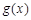 在
在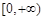 上无最大值(或:当
上无最大值(或:当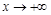 时,
时,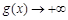 ),此时不满足条件;
),此时不满足条件;
②若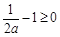 ,即
,即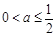 时,函数
时,函数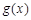 在
在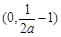 上单调递减,在区间
上单调递减,在区间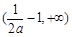 上单调递增,同样
上单调递增,同样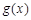 在
在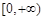 上无最大值,不满足条件.·························· 8分
上无最大值,不满足条件.·························· 8分
(ⅲ)当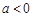 时,由
时,由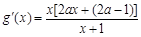 ,∵
,∵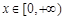 ,∴
,∴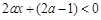 ,
,
∴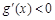 ,故函数
,故函数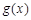 在
在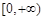 上单调递减,故
上单调递减,故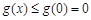 成立.
成立.
综上所述,实数a的取值范围是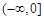 .··················· 10分
.··················· 10分
(Ⅲ)据(Ⅱ)知当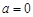 时,
时,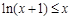 在
在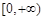 上恒成立(或另证
上恒成立(或另证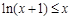 在区间
在区间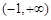 上恒成立), 11分
上恒成立), 11分
又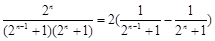 ,
,
∵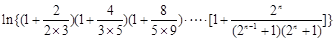
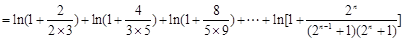
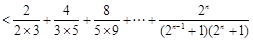
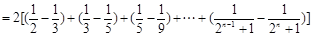
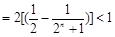 ,
,
∴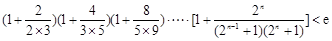 .··········· 14分
.··········· 14分
(1)因为当
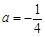 时,
时,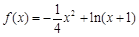 (
( ),
),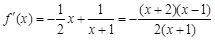 (
( ),
),由
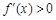 解得
解得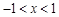 ,由
,由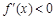 解得
解得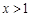 .得到单调区间。
.得到单调区间。(2)因函数
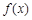 图象上的点都在
图象上的点都在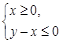 所表示的平面区域内,则当
所表示的平面区域内,则当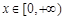 时,不等式
时,不等式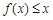 恒成立,即
恒成立,即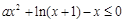 恒成立,设
恒成立,设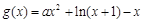 (
(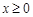 ),只需
),只需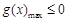 即可,转化思想的运用。
即可,转化思想的运用。(3)据(Ⅱ)知当
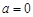 时,
时,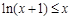 在
在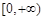 上恒成立(或另证
上恒成立(或另证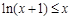 在区间
在区间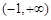 上恒成立)结合放缩法得到结论。
上恒成立)结合放缩法得到结论。(Ⅰ)当
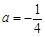 时,
时,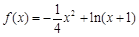 (
( ),
),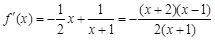 (
( ),
),由
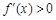 解得
解得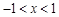 ,由
,由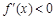 解得
解得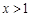 .
.故函数
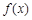 的单调递增区间为
的单调递增区间为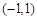 ,单调递减区间为
,单调递减区间为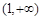 .········· 4分
.········· 4分(Ⅱ)因函数
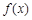 图象上的点都在
图象上的点都在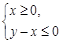 所表示的平面区域内,则当
所表示的平面区域内,则当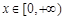 时,不等式
时,不等式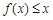 恒成立,即
恒成立,即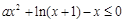 恒成立,设
恒成立,设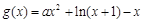 (
(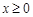 ),只需
),只需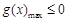 即可. 5分
即可. 5分由
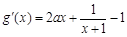
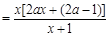 ,
,(ⅰ)当
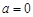 时,
时, 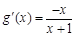 ,当
,当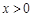 时,
时,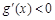 ,函数
,函数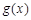 在
在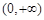 上单调递减,故
上单调递减,故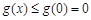 成立. 6分
成立. 6分(ⅱ)当
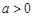 时,由
时,由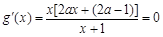 ,因
,因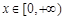 ,所以
,所以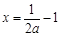 ,
,①若
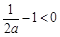 ,即
,即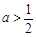 时,在区间
时,在区间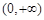 上,
上,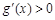 ,则函数
,则函数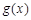 在
在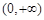 上单调递增,
上单调递增,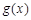 在
在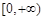 上无最大值(或:当
上无最大值(或:当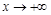 时,
时,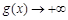 ),此时不满足条件;
),此时不满足条件;②若
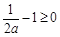 ,即
,即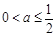 时,函数
时,函数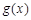 在
在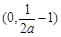 上单调递减,在区间
上单调递减,在区间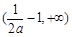 上单调递增,同样
上单调递增,同样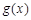 在
在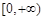 上无最大值,不满足条件.·························· 8分
上无最大值,不满足条件.·························· 8分(ⅲ)当
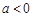 时,由
时,由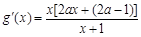 ,∵
,∵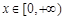 ,∴
,∴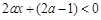 ,
,∴
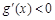 ,故函数
,故函数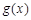 在
在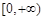 上单调递减,故
上单调递减,故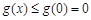 成立.
成立.综上所述,实数a的取值范围是
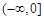 .··················· 10分
.··················· 10分(Ⅲ)据(Ⅱ)知当
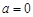 时,
时,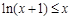 在
在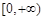 上恒成立(或另证
上恒成立(或另证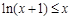 在区间
在区间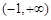 上恒成立), 11分
上恒成立), 11分又
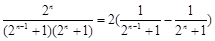 ,
,∵
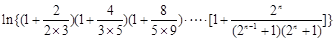
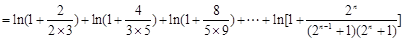
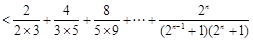
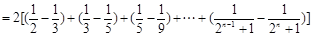
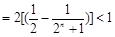 ,
,∴
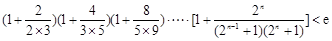 .··········· 14分
.··········· 14分
练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
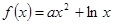 .
.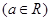
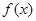 的单调性;
的单调性;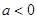 ,若函数
,若函数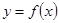 的图象总在直线
的图象总在直线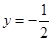 的下方,求
的下方,求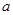 的取值范围;
的取值范围;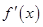 为函数
为函数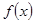 的导函数.若
的导函数.若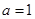 ,试问:在区间
,试问:在区间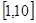 上是否存在
上是否存在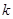 (
(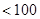 )个正数
)个正数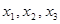 …
…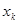 ,使得
,使得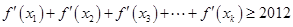 成立?请证明你的结论.
成立?请证明你的结论.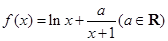 .
.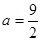 时,求
时,求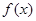 的极值;
的极值;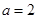 时,试比较
时,试比较 的大小;
的大小;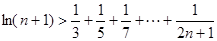 (
(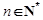 ).
).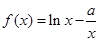 ;
;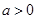 时,判断
时,判断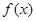 在定义域上的单调性;
在定义域上的单调性;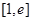 上的最小值.
上的最小值. ,
, ,
,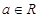 .
.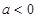 时,若函数
时,若函数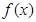 在区间
在区间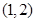 上是单调增函数,试求
上是单调增函数,试求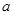 的取值范围;
的取值范围;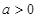 时,直接写出(不需给出演算步骤)函数
时,直接写出(不需给出演算步骤)函数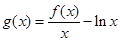 (
(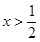 )的单调增区间;
)的单调增区间; ,使函数
,使函数 ,
,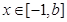 (
(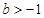 )在
)在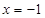 处取得最小值,试求实数
处取得最小值,试求实数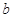 的最大值.
的最大值. 的导函数
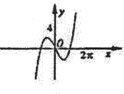
的导函数 的图象大致是( )
的图象大致是( )


 在(0,1)上是增函数.(1)求
在(0,1)上是增函数.(1)求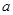 的取值范围;
的取值范围;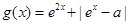 (
(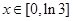 ),试求函数
),试求函数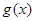 的最小值.
的最小值.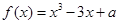 有3个不同的零点,则实数
有3个不同的零点,则实数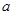 的取值范围是( )
的取值范围是( )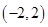
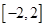
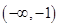
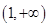
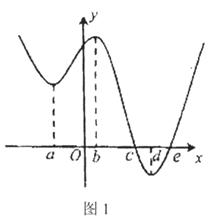
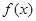 的导函数
的导函数 的大致图象如图所示,则下列结论一定正确的是
的大致图象如图所示,则下列结论一定正确的是